Тема 13. Элементы квантовой статистики

Квантовая статистика исследует системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

Пусть система состоит из N частиц. Состояние каждой частицы определяется координатами x,y,z и соответствующих проекций импульса p_x, p_y, p_z - 6 координат. Для N частиц - 6 N координат – это 6 N – мерное пространство называется фазовым.

Квантовая статистика, как и классическая изучает идеальный газ, так как реальную систему в хорошем приближении можно считать идеальным газом.

Электроны и другие частицы, у которых L_s – спин частиц равно нечетному числу, т.е. с полуцелым спином – фермионы, и подчиняются статистике Ферми-Дирака. С нулевым или целым спином – бозоны и подчиняются статистике Бозе-Эйнштейна.

Состояние системы невзаимодействующих частиц задается с помощью чисел заполнения N_i - числа, указывающие степень заполнения квантового состояния.

Для систем частиц, образованных бозонами N_i принимает любые целые числа 0,1,2….

Для систем частиц, образованных фермионами N_i принимает лишь два значения: 0 – для свободных состояний, 1 – для занятых состояний.

Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т.е. определить < N_i> - среднее число заполнения.

Идеальный газ из бозонов – бозе – газ описывается квантовой статистикой Бозе-Эйнштейна.

Распределение бозонов по энергиям имеет вид

- распределение Бозе-Эйнштейна

где < N_i> - среднее число бозонов в квантовом состоянии с энергией Е_i

k – постоянная Больцмана; Т – термодинамическая температура;

μ - химический потенциал, не зависит от энергии, а определяется только температурой и плотностью числа частиц. 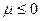- так как иначе < N_i> отрицательное, что не имеет смысла.

Идеальный газ из фермионов – ферми – газ описывается распределением Ферми-Дирака.

Распределение фермионов по энергиям имеет вид

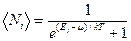- распределение Ферми-Дирака

μ - может иметь положительное значение.

Если , то распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Бозе-газ и ферми-газ – вырожденные газы, так как их поведение отличается от классического газа. Вырождение газов становится существенным при низких температурах и больших плотностях. Параметром вырождения является величина А. При 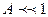, т.е. при малой степени вырождения, распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана.

Температура Т₀, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц - температура вырождения. Если 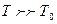поведение газа описывается классическими законами.

Дата добавления: 2014-01-04