
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7
ГЛАВА 3. ЭЛЕКТРОМАГНЕТИЗМ
3.1. Магнитное поле
Проводник с током представляет собой электрически нейтральную систему зарядов, в которой заряды одного знака движутся в одну сторону, а заряды другого знака - в противоположную (либо покоятся). Следовательно, проводник с током не имеет электрического поля. Однако, если поместить вблизи проводника магнитную стрелку, то она повернётся и займёт устойчивое положение. При изменении направления тока в проводнике магнитная стрелка поворачивается в противоположную сторону.
Вращение магнитной стрелки возможно только при действии на неё со стороны проводника, который образует вокруг себя силовое поле, называемое магнитным.
 Магнитное поле образуется движущимися зарядами и обнаруживается по повороту магнитной стрелки.
Магнитное поле образуется движущимися зарядами и обнаруживается по повороту магнитной стрелки.






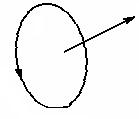 Подобно тому, как для исследования электрического поля используется пробный заряд, так и для исследования магнитного поля применяется замкнутый контур малых размеров с током I (пробный контур) (рис.3.1.). Магнитное поле оказывает на пробный контур ориентирующее действие. Контур с током поворачивается по вектору нормали
Подобно тому, как для исследования электрического поля используется пробный заряд, так и для исследования магнитного поля применяется замкнутый контур малых размеров с током I (пробный контур) (рис.3.1.). Магнитное поле оказывает на пробный контур ориентирующее действие. Контур с током поворачивается по вектору нормали 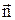 , который определяется по «правилу буравчика» (поступательное движение буравчика совпадает с вектором
, который определяется по «правилу буравчика» (поступательное движение буравчика совпадает с вектором 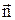 , вращательное – с направлением тока в конуре).
, вращательное – с направлением тока в конуре).
Нормаль, определённая по «правилу буравчика», называется положительной нормалью.
Пробный контур в магнитном поле занимает устойчивое положение, в котором его вектор нормали 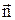 совпадает с направлением магнитного поля. Если контур повернуть на некоторый угол
совпадает с направлением магнитного поля. Если контур повернуть на некоторый угол 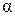 относительно направления поля, то возникает вращающий момент
относительно направления поля, то возникает вращающий момент 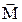 , возвращающий контур в прежнее устойчивое положение. Модуль вращающего момента
, возвращающий контур в прежнее устойчивое положение. Модуль вращающего момента 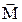 зависит от угла
зависит от угла 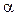 между нормалью контура и направлением поля, достигая наибольшего значения
между нормалью контура и направлением поля, достигая наибольшего значения 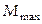 при
при 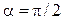 (при
(при 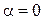 момент равен нулю).
момент равен нулю).
В одной и той же точке поля на разные пробные контуры при фиксированном угле 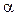 действует вращающий момент, который не зависит от формы контура, но пропорционален силе тока I в нём и площади S. Следовательно, действие магнитного поля на плоский контур с током определяется произведением I·S, которое называется дипольным магнитным моментом контура и обозначается Pm (аналогично вращающий момент, действующий в электрическом поле на диполь, пропорционален электрическому моменту диполя
действует вращающий момент, который не зависит от формы контура, но пропорционален силе тока I в нём и площади S. Следовательно, действие магнитного поля на плоский контур с током определяется произведением I·S, которое называется дипольным магнитным моментом контура и обозначается Pm (аналогично вращающий момент, действующий в электрическом поле на диполь, пропорционален электрическому моменту диполя 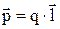 ).
).
Дипольный магнитный момент – векторная величина, совпадающая с направлением вектора положительной нормали контура и численно равна произведению его площади S на ток I в нём.
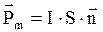 , (3.1)
, (3.1)
Модуль магнитного момента измеряется в [А·м2]
На пробные контуры, различающиеся значением 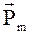 , в заданной точке поля действуют разные по модулю вращающие моменты М. Однако отношение модулей этих векторов оказывается при фиксированном угле
, в заданной точке поля действуют разные по модулю вращающие моменты М. Однако отношение модулей этих векторов оказывается при фиксированном угле 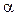 одним и тем же и определяет модуль магнитной индукции.
одним и тем же и определяет модуль магнитной индукции.
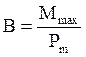 , (3.2)
, (3.2)
где Ммах – наибольшее значение вращающего момента контура, когда он повёрнут относительно направления поля на угол 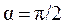 .
.
Магнитная индукция есть векторная величина, модуль которой определяется выражением (3.2), а направление задается равновесным положением положительной нормали контура с током.
Индукция магнитного поля в системе СИ измеряется в [Тл] – тесла.
Тесла – индукция магнитного поля, которое действует на плоский контур с магнитным моментом Рm=1 Ам2 и создаёт максимальный вращающий момент Мвр= 1Нм.
Учитывая векторный характер входящих в соотношение (3.2) величин, направление и модуль вращающего момента определяется соотношением
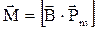 ,
, 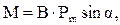 (3.3)
(3.3)
где 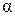 - угол между векторами
- угол между векторами 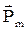 и
и 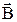 .
.
Опыт показывает, что для магнитного поля, как и для электрического,, справедлив принцип суперпозиции: индукция магнитного поля 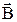 , образованного несколькими (n) движущимися зарядами (токами) в заданной точке пространства, равна векторной сумме индукций полей Вi, образованных зарядами (токами) в отдельности,
, образованного несколькими (n) движущимися зарядами (токами) в заданной точке пространства, равна векторной сумме индукций полей Вi, образованных зарядами (токами) в отдельности,
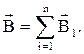
3.2. Линии индукции магнитного поля
Линиями индукции магнитного поля называют линии, касательные к которым совпадают с вектором индукции магнитного поля.
Линии индукции помогают представить картину магнитного поля и определить его величину и направление. Например, линии индукции магнитного поля прямолинейного проводника с током представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику, центр которых находится на оси проводника (рис. 3.2).
Линии индукции строят так, что их густота определяет величину вектора 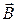 в данной точке поля. Направление силовых линий определяется по «правилу буравчика», в котором поступательное движение буравчика совпадает с направлением тока, а вращательное с направлением силовых линий. в данной точке поля. Направление силовых линий определяется по «правилу буравчика», в котором поступательное движение буравчика совпадает с направлением тока, а вращательное с направлением силовых линий.
| 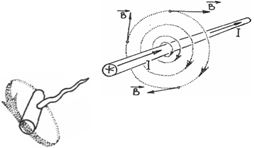 Рис. 3.2.
Рис. 3.2.
|
Важное свойство линий индукции состоит в том, что они всегда замкнуты или идут из бесконечности и уходят в бесконечность. Поле такого типа называют вихревым. Следовательно, магнитное поле - это вихревое поле.
Магнитное поле может быть однородным и неоднородным, стационарным и нестационарным.
Однородное поле – это поле, индукция которого во всех точках пространства одинакова, а линии индукции представляют прямые одного направления расположенные на одном расстоянии друг от друга.
Неоднородное поле – это поле, в котором от точки к точке меняется абсолютная величина и направление вектора 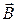 .
.
Стационарное магнитное поле – это поле, магнитная индукция которого не зависит от времени.
Нестационарное магнитное поле – это поле, магнитная индукция которого зависит от времени.
Вопросы и задания для самопроверки
1. В чем проявляется магнитное взаимодействие?
2. Как определяется направление индукции магнитного поля в заданной точке?
3. От каких параметров зависит модуль вектора индукции магнитного поля?
4. Дайте определение магнитного момента контура с током.
5. Определите момент сил действующих на рамку с током 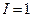 А и площадью S=1м2 в магнитном поле с B=1Тл, когда угол между векторами
А и площадью S=1м2 в магнитном поле с B=1Тл, когда угол между векторами 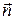 и
и 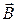 составляет 30º.
составляет 30º.
3.3. Закон Био-Савара – Лапласа
Индукция магнитного поля любого проводника с током I есть векторная сумма индукций полей 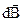 , создаваемых отдельными элементарными участками проводников , создаваемых отдельными элементарными участками проводников 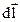 (элементами тока), и соответствует принципу суперпозиции (рис. 3.3).
Индукция магнитного поля (элементами тока), и соответствует принципу суперпозиции (рис. 3.3).
Индукция магнитного поля 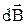 от элемента тока: от элемента тока: 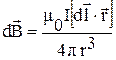 , , 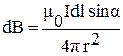 , (3.4) , (3.4)
| 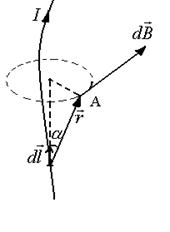 Рис. 3.3
Рис. 3.3
|
где 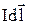 – элемент тока,
– элемент тока, 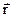 – радиус-вектор, проведенный от элемента тока в расчетную точку А;
– радиус-вектор, проведенный от элемента тока в расчетную точку А;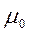 - магнитная постоянная;α - угол между векторами
- магнитная постоянная;α - угол между векторами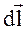 и
и 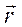 (рис.3.3).
(рис.3.3).
Исходя из принципа суперпозиции, для определения индукции магнитного поля в заданной точке от всего проводника с током длиной 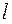 необходимо проинтегрировать вклады индукций от элементов тока:
необходимо проинтегрировать вклады индукций от элементов тока:
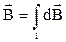 . (3.5)
. (3.5)
Для самостоятельного изучения
3.4. Магнитное поле прямолинейного проводника
Прямолинейные проводники имеют самое широкое распространение. Встречаются короткие и длинные проводники. В первом случае длина проводника, как правило, задана, во втором – не определена и считается бесконечной. Найдём индукцию магнитного поля в точке А, расположенной на расстоянии а от прямолинейного проводника с током I и длиной 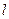 .
.
а) б)
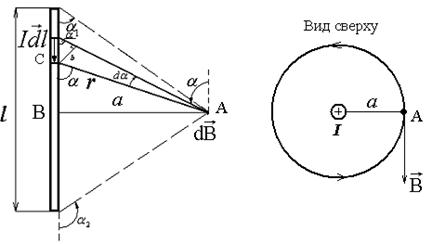
Рис.3.4.
Выделим в проводнике элемент тока (рис.3.4) и по закону Био–Савара–Лапласа определим индукцию магнитного поля от него в точке А:
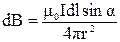 . (3.6)
. (3.6)
Так как в точке А все 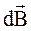 имеют одинаковые направления (рис.3.4б), то индукция магнитного поля по всей длине проводника определяется интегрированием dB
имеют одинаковые направления (рис.3.4б), то индукция магнитного поля по всей длине проводника определяется интегрированием dB
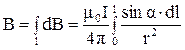 . (3.7)
. (3.7)
Выразим изменяющиеся величины r и 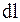 через одну угловую переменную
через одну угловую переменную 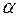 . Ввиду малости угла dα, длина перпендикуляра b, проведенного из конца элемента тока на радиус-вектор
. Ввиду малости угла dα, длина перпендикуляра b, проведенного из конца элемента тока на радиус-вектор 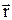 , равна: b=rdα. Из прямоугольного треугольника ABC модуль радиуса вектора
, равна: b=rdα. Из прямоугольного треугольника ABC модуль радиуса вектора 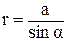 (рис.3.4а). Тогда
(рис.3.4а). Тогда
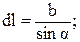
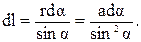

Подставим полученные значения в формулу (3.7):
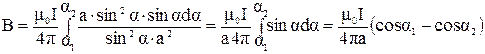 . (3.8)
. (3.8)
Для бесконечного проводника 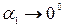 , а
, а 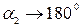 и, следовательно, в точке А индукция магнитного поля
и, следовательно, в точке А индукция магнитного поля
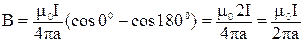 . (3.9)
. (3.9)
3.5. Магнитное поле на оси кольца с током
Круговые токи встречаются в катушках индуктивности и электромоторах, где проводники уложены в форме колец. Особый интерес представляют величина и направление вектора индукции магнитного поля на оси отдельного кольца c током в точке А, удаленной на расстоянии d от его центра (рис.3.5).
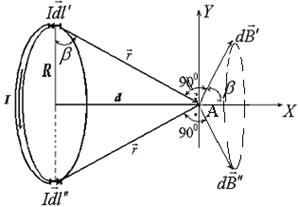
Рис.3.5
Выделим на кольце радиусом R симметричные элементы тока 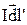
 и
и 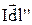 . По закону Био – Савара – Лапласа определим в точке А модуль вектора индукции магнитного поля от элемента тока
. По закону Био – Савара – Лапласа определим в точке А модуль вектора индукции магнитного поля от элемента тока 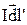
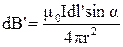
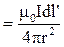 ,
,
где угол 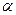 между векторами
между векторами 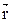 и I
и I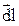 ' равен
' равен 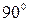 . Такое же значение по модулю индукция магнитного поля в точке А будет иметь от элемента тока I
. Такое же значение по модулю индукция магнитного поля в точке А будет иметь от элемента тока I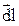 ".Векторы
".Векторы 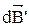 и
и 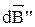 совпадают с касательными к линиям индукции магнитного поля от элементов тока
совпадают с касательными к линиям индукции магнитного поля от элементов тока 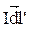 и
и 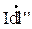 , проведенными через точку А. Проекции векторов
, проведенными через точку А. Проекции векторов 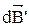 и
и 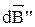 на ось OY по абсолютной величине равны и обратны по знаку, и поэтому при сложении они взаимно компенсируют друг друга. Следовательно, складываются только проекции векторов
на ось OY по абсолютной величине равны и обратны по знаку, и поэтому при сложении они взаимно компенсируют друг друга. Следовательно, складываются только проекции векторов 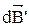 и
и 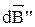 на ось OX. Тогда модуль индукции магнитного поля в точке А определяется интегрированием по всей длине l кольца:
на ось OX. Тогда модуль индукции магнитного поля в точке А определяется интегрированием по всей длине l кольца:
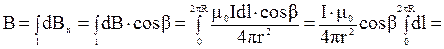
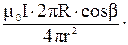
Из рис.3.5 следует, что 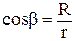 , а
, а 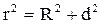 . Тогда индукция магнитного поля на оси кольца с током:
. Тогда индукция магнитного поля на оси кольца с током:
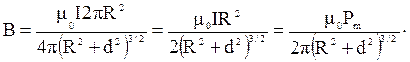 (3.10)
(3.10)
В центре кольца с током, когда 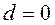 , индукция магнитного поля
, индукция магнитного поля
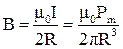 . (3.11)
. (3.11)
3.6. Магнитное поле на оси соленоида конечной длины
Рассмотрим соленоид с числом витков 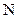 , радиусом , радиусом 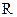 и длиной и длиной 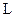 , по которому течет ток , по которому течет ток 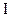 . Выделим на соленоиде на расстоянии . Выделим на соленоиде на расстоянии 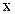 от его левого края бесконечно узкое кольцо шириной от его левого края бесконечно узкое кольцо шириной 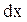 (рис 3.6).
Число витков в этом кольце dN=ndx, где (рис 3.6).
Число витков в этом кольце dN=ndx, где 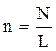 плотность витков соленоида. Сила тока в выделенном кольце плотность витков соленоида. Сила тока в выделенном кольце 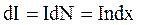 . .
| 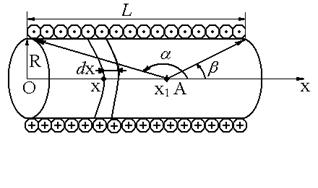 Рис.3.6
Рис.3.6
|
Направим ось ОХ вдоль оси соленоида, выбрав начало координат О на левом краю соленоида. В точке А с координатой 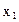 , которая отстоит от выделенного кольца с током dI на расстоянии
, которая отстоит от выделенного кольца с током dI на расстоянии 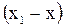 , модуль магнитной индукции согласно 3.10.
, модуль магнитной индукции согласно 3.10.
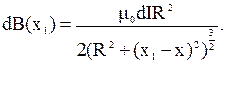
После подстановки 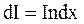 , получим
, получим
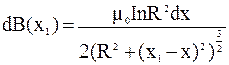
Модуль вектора магнитной индукции  в точке
в точке 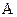 на оси соленоида определяется интегрированием dB(x1) по всей длине соленоида:
на оси соленоида определяется интегрированием dB(x1) по всей длине соленоида:
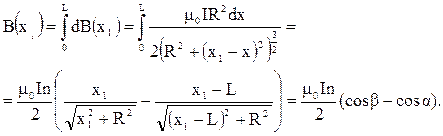 (3.12)
(3.12)
где α и β - углы между осью соленоида и радиус-вектором, проведенным из рассматриваемой точки к концам соленоида (рис.3.6).
В середине длинного соленоида 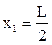 при длине
при длине 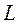 >>
>>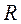 ,
,
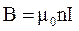 .
.
Вопросы и задания для самопроверки
1. В чём заключатся принцип суперпозиции для магнитного поля?
2. Определите понятие элемента тока
3. Напишите в векторной и скалярной форме закон Био-Савара-Лапласа.
4. Как определяется модуль вектора индукции магнитного поля для элемента тока и проводника с током?
5. Определите последовательность расчёта индукции магнитного поля от проводников конечной и бесконечной длины.
6. Определите зависимость модуля индукции магнитного поля кольца радиусом R=1 м и током I=1 А от расстояния d по его оси.
7. Определите индукцию магнитного поля В(х) на оси соленоида для х=2L (рис. 3.6)
3.7. Циркуляция вектора индукции магнитного поля. Закон полного тока
Интеграл 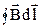 называется циркуляцией вектора индукции магнитного поля по замкнутому контуру.
называется циркуляцией вектора индукции магнитного поля по замкнутому контуру.
Для определения магнитной индукции с симметричным расположением витков с током вычисляется интеграл 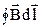 по замкнутому контуру вектора индукции магнитного поля
по замкнутому контуру вектора индукции магнитного поля 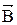 .
.
Найдем интеграл 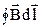 для контура l произвольной формы, лежащего в плоскости, перпендикулярной к бесконечному линейному проводнику с током I (рис. 3.7а)
для контура l произвольной формы, лежащего в плоскости, перпендикулярной к бесконечному линейному проводнику с током I (рис. 3.7а)
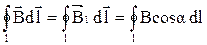 ,
,
где 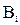 - проекция вектора
- проекция вектора 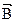 на направление обхода проводника с током на участке контура
на направление обхода проводника с током на участке контура  .
.
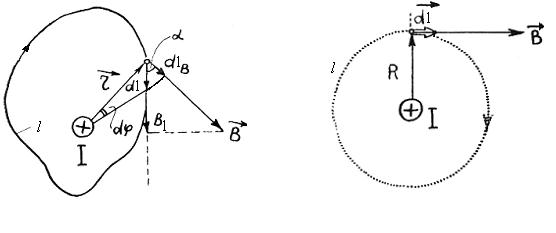
а б
Рис. 3.7
Из рис. 3.7а следует 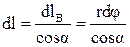 , где
, где 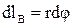 , т.к. угол
, т.к. угол 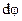 - бесконечно малый.
- бесконечно малый.
Тогда
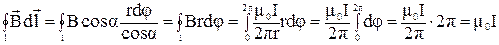 .
.
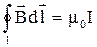 . (3.13)
. (3.13)
Результат интегрирования 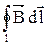 не зависит от формы контура. Например, для контура в виде окружности радиусом
не зависит от формы контура. Например, для контура в виде окружности радиусом 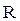 (рис. 3.7б) циркуляция вектора индукции магнитного поля прямолинейного проводника с током I равна
(рис. 3.7б) циркуляция вектора индукции магнитного поля прямолинейного проводника с током I равна
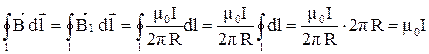 .
.
Пусть теперь произвольный контур l охватывает 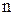 проводников с токами различного направления (рис. 3.8),
В этом случае, проводников с токами различного направления (рис. 3.8),
В этом случае, 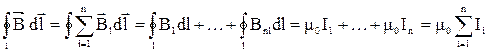 , ,
| 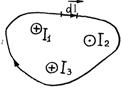 Рис. 3.8
Рис. 3.8
|
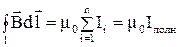 , (3.14)
, (3.14)
где 
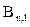 - проекция вектора индукции магнитного поля от
- проекция вектора индукции магнитного поля от 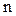 -го проводника с током на участке контура
-го проводника с током на участке контура 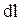 ,
, 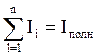 - полный ток, охватываемый контуром l.
- полный ток, охватываемый контуром l.
Ток считается положительным, если направление линий индукции его магнитного поля совпадает с направлением обхода контура и отрицательным, если не совпадает. В случае, указанном на рис. 3.8
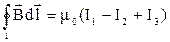 .
.
Соотношение (3.14) называют законом полного тока.
Если контур l охватывает N проводников с одинаковым током I, тогда в соответствии с равенствами (3.13)
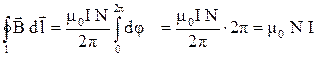 . (3.15)
. (3.15)
Для. самостоятельного изучения
3.8. Магнитное поле длинного соленоида
Равенство (3.15) можно применить для определения индукции магнитного поля в центре длинного соленоида, когда его длина L>>R (рис 3.6).
Пусть 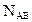 - число витков на участке - число витков на участке 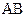 соленоида (рис 3.9), по которому течет ток I. Для вычисления индукции магнитного поля внутри соленоида запишем закон полного тока для прямоугольного замкнутого контура АВСDА, используя соотношение (3.15) соленоида (рис 3.9), по которому течет ток I. Для вычисления индукции магнитного поля внутри соленоида запишем закон полного тока для прямоугольного замкнутого контура АВСDА, используя соотношение (3.15)
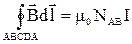 (3.16) (3.16)
| 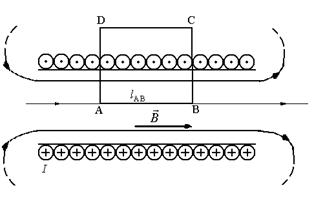 Рис. 3.9
Рис. 3.9
|
Интеграл 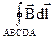 можно представить в виде суммы интегралов по участкам контура ABCDA
можно представить в виде суммы интегралов по участкам контура ABCDA
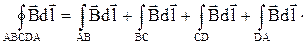
Первый интеграл в этой сумме равен ВlAB, где l АВ – длина участка АВ контура. Второй и четвертый интегралы равны нулю, так как вектор 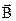 перпендикулярен векторам
перпендикулярен векторам 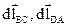 . Третий интеграл можно считать равным нулю, поскольку внешнее магнитное поле длинного соленоида практически отсутствует. Тогда
. Третий интеграл можно считать равным нулю, поскольку внешнее магнитное поле длинного соленоида практически отсутствует. Тогда
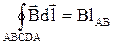 . (3.17)
. (3.17)
Из сравнения равенств (3.16), (3.17) следует, что
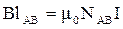 .
.
Решая последнее уравнение, относительно 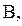 получим:
получим:
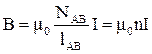 , (3.18)
, (3.18)
где 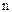 - число витков на единице длины соленоида.
- число витков на единице длины соленоида.
Следует отметить, что величина индукции магнитного поля не зависит от положения точки внутри соленоида, так как отрезок АВ не обязательно должен лежать на оси соленоида. Поле внутри длинного соленоида однородно, не зависит от формы витков, а направление его индукции параллельно оси соленоида.
3.9. Магнитное поле стержня с током
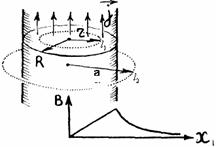
В стержне радиусом R течет постоянный ток с равномерно распределенной по сечению плотностью тока j. Определим зависимость индукции магнитного поля от расстояния, а от оси стержня.
Учитывая, что j = I/S,  запишем полный ток в стержне
запишем полный ток в стержне
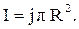
Вычислим модуль вектора индукцию магнитного поля 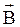 внутри стержня. Для этого рассмотрим контур интегрирования в виде окружности радиусом
внутри стержня. Для этого рассмотрим контур интегрирования в виде окружности радиусом 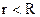 (рис.3.10). Закон полного тока
(рис.3.10). Закон полного тока
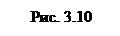
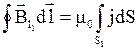 , (3.19)
, (3.19)
где 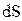 - элемент площади S поперечного сечения стержня радиусом r.
- элемент площади S поперечного сечения стержня радиусом r.
После интегрирования левой и правой части равенства с учетом того, что плотность тока не изменяется, а индукция В каждой точке контура постоянна по модулю
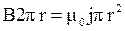 ,
,
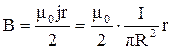 .
.
Внутри стержня магнитное поле увеличивается с расстоянием от оси по линейному закону, достигая максимального значения на поверхности.
Для расчета магнитной индукции вне стержня возьмем контур интегрирования 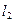 в виде окружности радиусом а>R. Закон полного тока запишем в виде
в виде окружности радиусом а>R. Закон полного тока запишем в виде
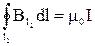 .
.

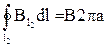 , так как индукция В в каждой точке контура l2, постоянна по модулю, следовательно
, так как индукция В в каждой точке контура l2, постоянна по модулю, следовательно 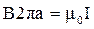 , a
, a
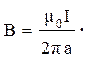 (3.20)
(3.20)
Из сравнения соотношений (3.20) и (3.9) следует, что вне стержня магнитное поле оказывается таким, как если бы полный ток протекал по оси стержня. Зависимость модуля индукции магнитного поля от расстояния от оси стержня представлена на рис. 3.10.
Вопросы и задания для самопроверки
1. Что называют циркуляцией вектора индукции магнитного поля?
2. Дайте определение закона полного тока.
3. Запишите закон полного тока для контура, охватывающего проводник n раз?
4. Запишите закон полного тока для контура, охватывающего n проводников?
5.Определите циркуляцию 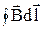 по замкнутому контуру в виде
по замкнутому контуру в виде
равностороннего треугольника, в центре которого, находится проводник с током I.
6. Составьте алгоритм расчета индукции магнитного поля с помощью
вычисления интеграла 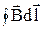 .
.
7. Определите зависимость индукции магнитного поля от
расстояния от оси стержня радиусом 10 см, по которому течёт ток I=1A.
3.10. Сила Лоренца
Опытным путем установлено, что на заряд q, движущийся со скоростью 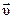 в магнитном поле с индукцией
в магнитном поле с индукцией 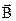 , действует сила
, действует сила
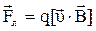 . (3.21)
. (3.21)
Эта сила была названа силой Лоренца. Модуль вектора силы 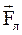 определяется
определяется
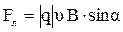 , (3.22)
, (3.22)
где 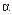 - угол между векторами
- угол между векторами 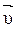 и
и 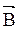 .
.
Из уравнений (3.21) и (3.22) следует три важных вывода, связанных с величиной и направлением силы 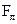 :
:
а) сила Лоренца в магнитном поле действует только на движущиеся заряды, т. е. если заряд q покоится (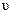 =0), то
=0), то 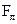 =0;
=0;
б) сила Лоренца 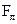 всегда перпендикулярна векторам всегда перпендикулярна векторам 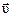 и и 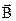 , т.е. , т.е. 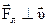 ; ; 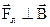 (рис. 3.11). Векторы (рис. 3.11). Векторы 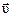 и и 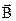 . лежат в плоскости S, а сила . лежат в плоскости S, а сила 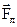 перпендикулярна этой плоскости. Направление силы Fл зависит от знака заряда q и от взаимного расположения векторов перпендикулярна этой плоскости. Направление силы Fл зависит от знака заряда q и от взаимного расположения векторов 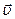 и и 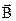 . .
| 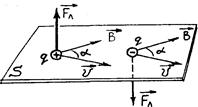 Рис. 3.11
Рис. 3.11
|
Изменение знака заряда приводит к смене направления силы Лоренца на противоположное.
в) модуль силы Лоренца зависит от угла 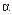 между векторами между векторами 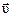 и и 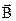 , , 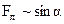 (рис. 3.12). В частности, если (рис. 3.12). В частности, если 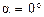 или или 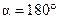 , то , то 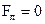 . Это означает, что на заряды, движущиеся вдоль линий магнитного поля . Это означает, что на заряды, движущиеся вдоль линий магнитного поля 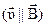 , не действует сила , не действует сила 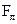 . Магнитное поле действует только на заряды, движущиеся под некоторым углом к его линиям индукции. . Магнитное поле действует только на заряды, движущиеся под некоторым углом к его линиям индукции.
| 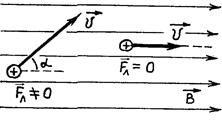 Рис. 3.12
Рис. 3.12
| |
Направление силы Лоренца можно определить по правилу левой руки: левую руку располагают так, чтобы силовые линии индукции входили в ладонь, четыре вытянутых пальца указывали направление движения положительного заряда, тогда отогнутый на  большой палец указывает направление силы Лоренца (рис.3.13). большой палец указывает направление силы Лоренца (рис.3.13).
| 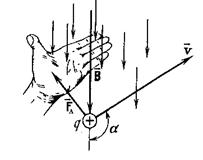 Рис. 3.13.
Рис. 3.13.
| |
3.11. Закон Ампера
Если проводник с током I находится в магнитном поле, то на каждый его электрон (носитель тока) действует сила Лоренца
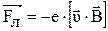 ,
,
где 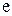 – модуль заряда электрона,
– модуль заряда электрона, 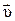 – скорость направленного движения электрона в электрическом поле проводника.
– скорость направленного движения электрона в электрическом поле проводника.
Сила Лоренца, действуя на носители тока в проводнике, перемещает его в магнитном поле. Найдем направление и модуль этой силы.
Выделим в проводнике c током I (рис.3.14.) элемент тока 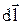 , а силу, действующую на него, представим в виде
, а силу, действующую на него, представим в виде
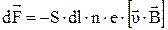 ,
,
где S – площадь поперечного сечения проводника, n-число носителей тока в единице объема проводника, S·dl·n – число носителей тока в объеме проводника длиной dl.
Произведение величин –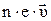 - есть плотность тока
- есть плотность тока 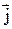 , которая по модулю равна заряду, протекающему через единичное сечение проводника в единицу времени. В связи с этим последнее равенство можно записать в виде
, которая по модулю равна заряду, протекающему через единичное сечение проводника в единицу времени. В связи с этим последнее равенство можно записать в виде
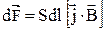
Так как направления векторов 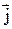 и
и 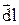 совпадают и, следовательно,
совпадают и, следовательно, 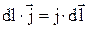 , то
, то
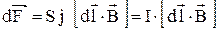 , (3.23)
, (3.23)
где 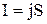 по определению плотности тока.
по определению плотности тока.
Сила 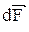 называется силой Ампера и обозначается называется силой Ампера и обозначается 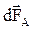 .
Модуль вектора силы Ампера .
Модуль вектора силы Ампера
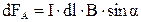 , (3.24)
где , (3.24)
где 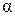 - угол между векторами - угол между векторами 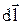 и и 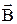 .(рис.3.14) .(рис.3.14)
| 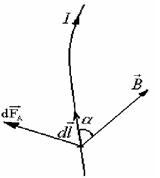 Рис. 3.14. Рис. 3.14.
|
Элементарная сила 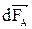 направлена перпендикулярно плоскости, в которой лежат векторы
направлена перпендикулярно плоскости, в которой лежат векторы 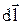 и
и 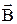 . Сила, действующая на проводник длиной
. Сила, действующая на проводник длиной 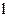 , определяется в результате интегрирования
, определяется в результате интегрирования 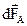 по всей длине проводника
по всей длине проводника
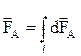 .
.
Направление силы Ампера можно определить по правилу левой руки.
Левую руку располагают так, чтобы силовые линии магнитного поля входили в ладонь, четыре вытянутых пальца указывали направление тока в проводнике, тогда отогнутый на 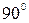 большой палец указывает направление силы Ампера (рис. 3.15). большой палец указывает направление силы Ампера (рис. 3.15).
| 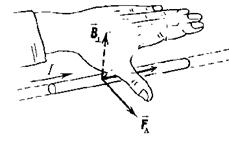 Рис. 3.15
Рис. 3.15
|
Вопросы и задания для самопроверки
1. Что называют циркуляцией вектора индукции магнитного поля?
2. Дайте определение закона полного тока.
3. Назовите условия возникновения силы Лоренца.
4. Как определить направление и модуль силы Ампера?
5.Запишите правило левой руки для определения направления силы Лоренца и Ампера.
|
|
Дата добавления: 2013-12-11; Просмотров: 1858; Нарушение авторских прав?; Мы поможем в написании вашей работы!