Плотность вероятности

Построим график P(xi) для условий Задачи 1 (Рис. 2).

Вычисляем локальную вероятность для каждой зоны

P_i = P (x_i - Δ /2 < Х < x_i + Δ /2) = n_i /N, i = 1… L, (2)

где n_i – количество точек, попадающее в зону i, включая левую границу.

Отметим, что в курсе принимается частотное определение вероятности, а не, например, «временное». Здесь используется прием разбиения на классы – интервалы. (Аналогия - шкала интервалов и порядка СИ, формирование классов производится с использованием отношения эквивалентности и предпочтения (≈, )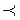

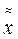( _i) = (x: х_{gi – 1} Х х_gi), i = 1 …L.

P_i можно рассматривать как долю результатов, имеющих дискретное значение 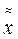_i.

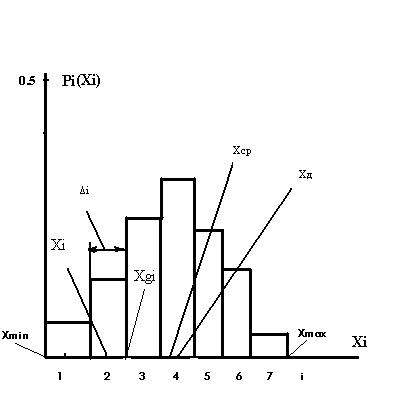
Рис. 2.

Гистограмма P (x_i)

Свойства P (x_i):

1) P (x_i) имеет малые значения на периферии,

P (x ₄) ≈ max при x_i ≈ x _д ≈ x _ср, поэтому x _д ≈ x _ср является наиболее вероятным значением среди других классов; форма P (x_i) напоминает ступенчатую «Шляпу»,

2) площадь S под линией равна 1, то есть

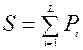= Σ n_i /N = 1.

Функция распределения F ( x )

Введем термин «накопленная вероятность» или функция распределения F (x_k) для дискретной величины, она определяется и вычисляется по следующему правилу

F (x ₁) = P (x ₁), F (x ₂) = P (x ₁) + P (x ₂), … F (x_k) = 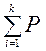(x_i). (4)

Функция распределения F (x_i) (характеристика №1) представляет собой вероятность Р для интервала

x_min < Х < x_i + Δ /2

в виде

F (x_i) = (n ₁ + n ₂ + n ₃ … + n_i)/ N = P (x_min < Х < x_i + Δ /2). (5)

F (x_i) в форме (5) представляет собой эмпирическую функцию распределения или F_exp.

Построим график F (x_i), i = 1… L. Для этого используем P (x_i) (Рис. 2) для условий Задачи 1. В итоге получаем зависимость F (x_i) (Рис. 3).

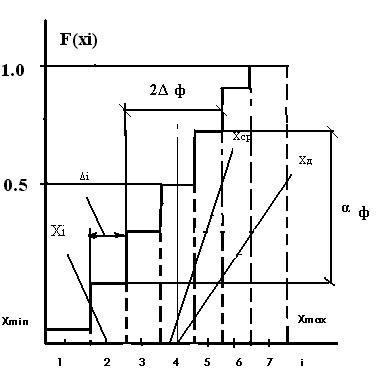
Рис. 3.

Функция распределения F (x_i)

Отметим значения в характерных точках F (x ₄) ≈ 0.5, F (x ₇) = 1.

Если F (x_i) является известной, то с помощью нее можно определить:

1) локальную вероятность попадания Х в к – интервал

Р (x _к) = F (x_к) - F (x _к-1), (5)

2) рассчитать среднее значение или действительное значение Х по следующему соотношению

x _ср = Σ x_i P (x_i) = Σ x_i (F (x_i) - F (x _i-1)), i = 1… L (6)

3) долю точек α _ф, которая попадает в заданное фиксированное поле 2 Δ_ф в окрестности x _ср.

Введем два поля:

а) поле допуска 2Δ_фдля значений х, которые отвечают условию

x _ср - Δ_ф < х < x _ср +Δ_ф

где Δ_ф - доверительный интервал Δ_дов = Δ_ф,

б) доверительную вероятность α _дов в виде

α _дов = α _ф = F (x _cр + Δ_ф) - F (x _cр - Δ_ф).

Например, для нормального распределения Х Î N (σ,A) являются распространенными следующие границы, связанные с параметром σ = СКО – средним квадратическим отклонением

.

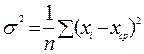Для таких интервалов применяются следующие оценки

Δ_ф = σ, α _ф ≈ 68 %,

Δ_ф = 3σ, α _ф ≈ 99 %.

Как изменится F (x_i), если L → ∞, Δ_i = D/L → 0и N → ∞?

F (x) становится сглаженной (высота ступеней - Р (x _к) уменьшится). В произвольной точке x функция F (x) определяет долю точек n / N, попадающую в интервал x_min < Х < x, или вероятность

F (x) = n / N = P (x_min < Х < x). (6)

Форма F (x) (характеристика №1) напоминает «Склон» (Задача 1, Рис. 3).

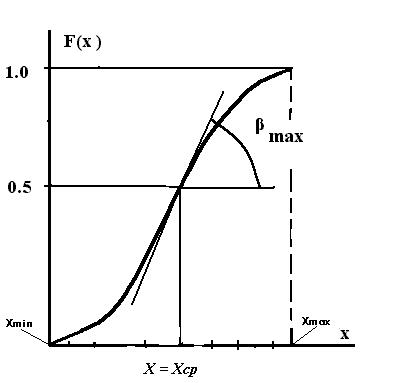
Рис. 3.

Эмпирическая функция распределения F (x) (Пример 1)

В точке x = x _ср выполняются условия

F (х = x _ср) ≈ 0.5, 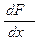= tgβ_max = f (х = x _ср),

где f (х = x _ср) – производная 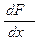в точке x _ср или плотность вероятностей.

Рассмотрим F (x_i) на Рис. 3 и введем плотность вероятности f (x) (характеристику №2) в форме отношения локальной вероятности P (x_k) к ширине зоны Δ_k

f (x_k) 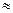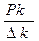= (F (x_k) - F (x _к-1))/(x_к - x _к-1)= 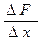= 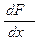(7)

Если построить график f (x_i), то он будет подобным гистограмме P (x _i). Отличие f (x_i) от P (x_i) связано с постоянным делителем Δ_k, который приводит к тому, что f (x_i) является размерной величиной.

Как изменится f (x_i), если L → ∞ и Δ_i = D/L → 0?

Форма f (x_i) будет гладкой (высота ступеней уменьшится), она напоминает «Шляпу» (Задача 1, Рис. 5)

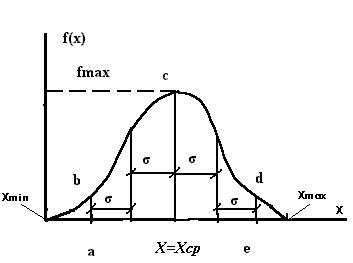
Рис. 5.

Плотность вероятности f (x)

В заданной точке f (x) определяет производную от функции распределения F (x) по определению

f (x) = 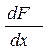. (8)

В точке x = x _ср выполняется условие

f (х = x _ср) ≈ f _max.

Это означает, что x _ср доставляет наибольшую плотность вероятности или x _ср является наиболее вероятным значением случайной величины Х.

Если f (x) является известной, то с ее помощью можно решать следующие задачи:

1) определить функцию распределения F (х), используя соотношение

F (х) = ,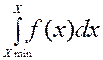

2) рассчитать среднее значение или действительное значение Х можно определить по следующему соотношению

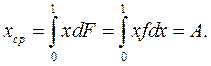(9)

3) рассчитать долю точек α _ф, которая попадает в заданный фиксированный интервал Δ_ф в окрестности x _ср, используя связи

α _ф = F (x_a = x _cр + Δ_ф/2) - F (x_е = x _cр - Δ_ф/2) = .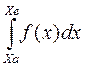

4) записать результат индивидуального измерения как

Х = А ± D _ф /2 = x _cр ± D _ф /2 при α = α _ф.

Дата добавления: 2013-12-11