Нер-во Коши-Буняковского

Евклидовы пространства

Алгоритм нахождения собств векторов и значений

1. Находим собственное значения решая характ Ур-ние det | A - λE |=0
2. Записываем систему для нахождения собственных векторов | A - λE |х=0
3. Подставляя в эту систему найденные λ находим собств вектора – ФСР однородн системы. Число собств векторов отвечающих λ=λ₁ равна n-r_i, где r_i=rg(A-λ_iE)

Лекция 10

Опр: В линейном пространстве L задано скалярное произв если каждой паре векторов (x,y)ÎL поставлено в соответствие число (х,у) так что выполняются аксиомы:(х,у,z,0 - векторы)

1. (x,y)= (y,x)

2. (ax,y)= a(x,y)

3. (x+y,z)= (x,z)+ (y,z)

4. (x,x)>0 если х¹0

5. (x,x)=0 если x=0

Опр: Линейное пространство L со скалярным произведением называют Евклидовым пространством.

В пространстве R_n скал прозвед обычно задают так (x,y)=x₁y₁+x₂y₂+…+x_ny_n. Легко проверить что все оксиомы выполняются. Простр R_n с таким скал произведением обозначают E_n.

Для любых векторов x,yÎL справедливо нер-во: (x,y)²£(x,х)(у,y) (1)

Док-во: (ax-y,ax-y)³0

a²(x,x)-2a(x,y)+(y,y)³0

Т.к. он принимает только неотр значения то дискриминант D’=D/4£0

D’=(b/2)²-ac=(x,y)²-(x,x)(y,y)£0 из этого следует неравенство (1)

Опр: Нормой (длиной) вектора хÎL назыв число ççхçç=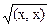

Свойства норм:

1. ççхçç³0 ççхçç=0 Û х=0
2. ||ax||=|a|*||x||
3. ||x+y||£||x||+||y|| нер-во треугольника

Докажем (3)

Нер-во коши-Буняковского можно записать и так |(x,y)|=||x||*||y||

||(x,y)||²=(x+y,x+y)= (x,x)+2(x,y)+ (y,y)£||x||²+2||x||*||y||+||y||²=(||x||+||y||)² отсюда ||(x,y)||£||x||+||y||

угол между векторами х,уÎL назыв угол fÎ[0,p] cosf=((x,y)/(||x||*||y||)). Из нер-ва К-Б следует что правая часть всегда £1.

Опр: Вектора x,y наз ортоган если (x,y)=0. пишут х^у

Докажем теорему Пифагора: Если х^у то ||x+y||=||x||2+||y||2

Док -во: ||x+y||2==(x+y,x+y)= (x,x)+2(x,y)+ (y,y)= ||x||²+||y||²

Опр: Система вектр х₁,х₂.х₃..х_n наз ортогона если все вектора системы попарно ортоган-ны: (x_i,y_j)=0 i¹j

Лемма: ортоган система линейна независима

Док-во: Запишем рав-во: a₁х₁+a₂х₂+….a_nx_n=0 (1) умножим скалярно на х₁ получим a₁(x₁,x₁)=0 Þ a₁=0 аналогично доказыв а₂=а₃=а_n=0

Опр: Система вектр х₁,х₂,х₃..х_n наз ортонормир если все вектора системы попарно ортоган-ны и их нормы =1

(x_i,y_j)=0 i¹j

(x_i,y_j)=1 i=j

Вектор с нормой 1 назыв единичным, для произв вектора х вектор е=(х/||x||) явл единичным.

Умножение вектора на множитель 1/||x|| назыв нормировкой

Дата добавления: 2013-12-12