Нахождение Собственных векторов и собств значений

Характеристическийй многочлен оператора

Инвариантные подпространства

Свойства Собственных векторов и собств значений

Собственные вектора и собственные значения

Опр. Не нулевой вектор х называется собственным вектором оператора А, если найдется такое число λ, что выполняется равенство: А х = λ х, число λ называется собственным значением оператора А.

1. Каждому собственному вектору соответствует только одно собств значение

Док-во: предположим противное Ах=λх, Ах=λ₁х вычитая их друг из друга получим 0=(λ-λ₁)х значит λ=λ₁

1. Если х собственный вектор отвеч λ то и a х также собственный вектор отвеч λ.

Док-во: Пусть Ах=λх тогда А(a х)= a Аλх= a λх=λ(a х) т.е. А(a х) =λ(a х)

1. Если х₁ и х₂ собствен вектора отвеч λ то их сумма х₁+х₂ также собственнй вектор

Док-во: Ах₁=λх₁, Ах₂=λх₂ тогда А(х₁+х₂)=Ах₁+Ах₂=λх₁+λх₂=λ(х₁+х₂)

Более общее св-во: Если х₁,х₂,,,х_к- собств вектора, отвеч λ то любая их линейн комбин также собственный вектор отвеч λ.

1. Собств вектора отвеч различным собственным знач линейнонезависимы

Докажем для 2-х векторов: Ах=λ₁х Ау=λ₂ у λ₁¹λ₂ Покажем что х и у лин независимы Предположим противное т.е. что они зависимы тогда у=λх Из св-ва (2) следует что у отвечает собственному знач λ₁(противоречие).

В общем случ док-ся методом мат индукции.

Подпр-во L₁ÎL наз инвариант подпростр оператора А если "хÎL₁, АхÎL₁. Из св-в (2) и (3) следует что множество векторовотвечающих одному собств знач λ образ инвариантное пр-во.

Характеристическийй многочлен оператора А называется определитель det | A - λE | где А матрица оператора в некотором базисе 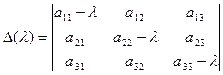В n-мерном пр-ве характерист многочлен явл многочлен степени n относительно λ

Характеристич уравнением называется Ур-е D λ =det | A - λE |

Теорема(инвариантность характеристич многочлена): Характеристическийй многочлен не зависит от выбора базиса

Док-во: Пусть А и А’=Т^-1АТ матрицы операторов в разл базисах. Т – матрица перехода.

det(A’ - λE) = det(T^-1AT - λT^-1T) = det[T^-1(A - λE)T] = detT^-1det(A - λE)detT = det(A - λE).

Det(A’ - λE) = det(A - λE)

Теорема: Если оператор А имеет собственное значение, то они явл корнями характиристич многочлена

Пусть Ах=λх (1) это рав-во можно записать в виде (А-λЕ)х=0 (2). В коорд записи ур-е (2) есть система однородн линейных уравнений 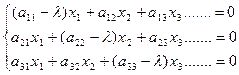Эта система имеет не тривиальное решение если опред матрицы системы = 0 (Из Т Крамера). Отсюда det | A - λE |=0 т.е. λ – корень характеристич многочлена.

В вещ пространстве оператор А может не иметь собств знач т.к. корни характеристич многочлена могут быть комплексными.

Дата добавления: 2013-12-12