I итерация

Исходная симплекс-таблица

Таблица 5.10

Симплекс-таблица IV итерации

Таблица 5.9

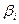
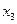
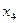
СП БП				Оценочные отношения
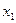
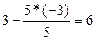
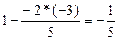
			–(–3/5)=3/5
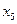
	5/5=1	–2/5	(5)^–1=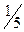
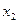
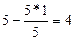
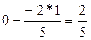
			–(1/5)=–1/5
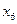
			–(9/5)=–9/5
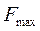
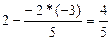
			–(–3/5)=3/5

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:

.

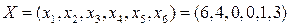3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи 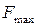=24, которое достигается при .

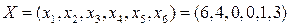Пример 5.5. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:

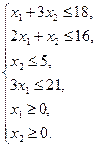
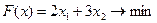
Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

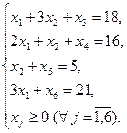
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х₃, х₄, х₅, х₆, тогда свободными переменными будут х₁, х₂. Выразим базисные переменные через свободные:

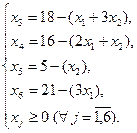
Приведем целевую функциюк следующему виду:

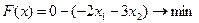
На основе полученной задачи сформируем исходную симплекс-таблицу:

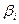
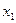
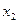
СП БП				Оценочные отношения
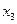
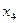
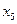
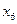
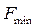
		–2	–3

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

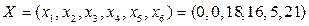3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи 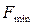=0, которое достигается при .

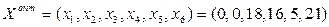Пример 5.6. Решить следующую задачу линейного программирования симплекс-методом:

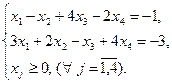
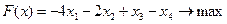
Решение:

1 этап: составление исходной симплекс-таблицы.

Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х₁ и х₂.

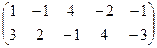
Умножим (поэлементно) первую строку на –3 и сложим со второй:

.

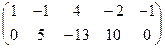Умножим вторую строку на :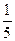

.

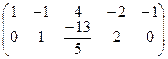Сложим вторую с первой строкой:

.

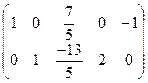В результате система ограничений примет следующий вид:

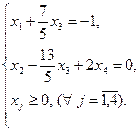
Выразим базисные переменные через свободные:

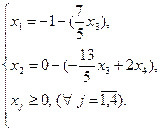
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

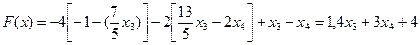Запишем целевую функцию в следующем виде:

.

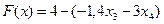Составим исходную симплекс-таблицу:

Дата добавления: 2013-12-12