Двойственные задачи ЛП

Исходная симплекс-таблица

Таблица 5.11

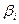
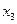
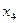
СП БП				Оценочные отношения
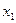
	–1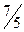
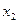
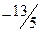
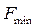
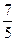
		–	–3

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

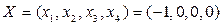Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х₂, равная нулю.

3 этап: проверка совместности системы ограничений ЗЛП.

Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.

Предприятие выпускает n видов продукции (P₁, P₂, …, P_n) используя для производства m видов ресурсов (S₁, S₂, …, S_m). Известны данные о нормах расхода ресурсов на единицу продукции каждого вида и их запасах на предприятии, т.е.: – норма расхода ресурса S_i для производства единицы продукции P_j; 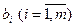– запас ресурса S_i на предприятии.

Цена единицы продукции P_j составляет .

Необходимо составить такой план производства продукции, при котором выручка от ее реализации была бы максимальной.

Обозначим через – объем продукции P_j, запланированный к производству – искомые величины. Тогда математическая модель данной задачи будет иметь следующий вид:

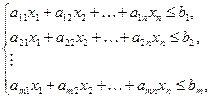(5.29)

(5.30)

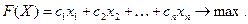(5.31)

Полученная задача, является задачей линейного программирования, записанной в стандартной форме. Для удобства задачу (5.29)–(5.31) можно представить в компактной форме:

(5.32)

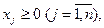(5.33)

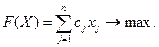(5.34)

В итоге математическая модель задачи планирования производства может быть сформулирована следующим образом: составить такой план производства продукции X =(x₁, x₂, …, x_n), удовлетворяющий системе ограничений (5.32), условию (5.33), при котором целевая функция (5.34) принимает наибольшее значение.

Предположим, что некоторая организация решила закупить у предприятия ресурсы S₁, S₂, …, S_m и ей необходимо определить оптимальные цены на эти ресурсы y₁, y₂, …, y_m, исходя из следующих условий:

1) общая стоимость ресурсов для закупающей организации должна быть минимальной;

2) за каждый вид ресурса предприятию надо уплатить не менее той суммы, которую оно может получать при переработке данного вида ресурса в готовую продукцию.

Исходя из условия 1 покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах b₁, b₂, …, b_m по ценам соответственно y₁, y₂, …, y_m были минимальными, т.е.

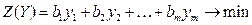. (5.35)

Исходя из условия 2 для удовлетворения требований продавца стоимость ресурсов, потребляемых при изготовлении единицы продукции каждого вида, должна быть не меньше ее цены, т.е.

(5.36)

По свой сущности переменные y_i не отрицательные, т.е.

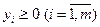. (5.37)

Таким образом, математическая модель для закупающей организации будет иметь следующий вид:

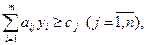(5.38)

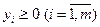, (5.39)

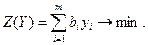(5.40)

Сравним математические модели (5.29) – (5.31) и (5.38) – (5.40):

1) число неизвестных одной задачи равно числу ограничений другой;

2) матрица коэффициентов системы ограничений одной задачи получается путем транспонирования матрицы коэффициентов системы ограничений другой задачи;

3) неравенства в системах ограничений имеют противоположный смысл;

4) свободные числа системы ограничений одной из задач являются коэффициентами при неизвестных в целевой функции другой задачи и наоборот;

5) целевые функции в задачах имеют противоположный смысл.

Задачи линейного программирования, обладающие пятью вышеуказанными формальными признаками, называют симметричнойдвойственной парой, причем одну из них (исходную) принимают в качестве основной, а другую – двойственной.

В теории линейного программирования выделяют также и несимметричныедвойственныепары, к примеру, если системы ограничений задач содержат ограничения-равенства и/или отсутствуют условия неотрицательности переменных.

Правила построения двойственной пары:

1) Знаки неравенств в системе ограничений исходной задачи приводятся в соответствие с ее целевой функцией, т.е. если она минимизируется, то неравенства должны иметь вид «≥», а если максимизируется, то «≤». Данный принцип распространяется и на двойственную задачу.

2) Определяется число неизвестных параметров двойственной задачи, равное числу ограничений исходной задачи.

3) Определяется область допустимых значений каждой из переменных двойственной задачи исходя из следующего правила:

каждому i -му ограничению-неравенству исходной задачи соответствует i -ая переменная двойственной задачи, удовлетворяющая условию неотрицательности; а каждому i -му ограничению-равенству исходной задачи соответствует i -ая переменная двойственной задачи, неограниченная по знаку.

4) Определяется матрица коэффициентов системы ограничений двойственной задачи путем транспонирования матрицы коэффициентов системы ограничений исходной задачи.

5) Определяются свободные числа системы ограничений двойственной задачи, равные коэффициентам при неизвестных в целевой функции исходной задачи.

6) Записывается система ограничений двойственной задачи, причем вид каждого ограничения определяется исходя из следующего правила:

каждой j -ой переменной исходной задачи, удовлетворяющей условию неотрицательности, соответствует j -ое ограничение-неравенство двойственной задачи (вид неравенства устанавливается в соответствие с принципом сформулированном в правиле 1 и исходя из того, что целевая функция двойственной задачи имеет противоположный целевой функции исходной задачи смысл (правило 7)); а каждой j -ой переменной исходной задачи, неограниченной по знаку, соответствует j -ое ограничение-равенство двойственной задачи.

7) Определяются коэффициенты при неизвестных целевой функции двойственной задачи, равные соответствующим свободным числам системы ограничений исходной задачи. Затем записывается целевая функция двойственной задачи, причем она будет иметь противоположный целевой функции исходной задачи смысл, т.е. минимизироваться, если целевая функция исходной задачи максимизируется и, наоборот.

Пример 5.7. Составить двойственную к следующей задаче линейного программирования:

.

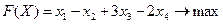В соответствии с правилом 1 приводим систему ограничений в соответствие с целевой функцией (умножаем первое ограничение на –1), тогда исходная задача будет иметь вид:

,

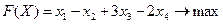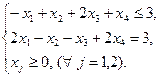
В соответствии с правилом 2 вводим две переменные y₁ и y₂, причем, исходя из правила 3, y₁ ≥ 0, а переменная y₂ не ограничена по знаку.

Определим матрицу коэффициентов системы ограничений двойственной задачи исходя из правила 4:

.

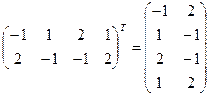В соответствии с правилом 5 компонентами вектора свободных чисел являются соответствующие коэффициенты при неизвестных целевой функции исходной задачи, т.е.

.

Запишем систему ограничений двойственной задачи:

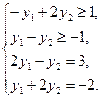
Первое и второе ограничение имеют вид неравенства в силу того, что переменные x₁ и x₂ удовлетворяют условию неотрицательности, а знак «≥» определяется правилами 1 и 7. Переменные x₃ и x₄ не ограничены по знаку, поэтому третье и четвертое ограничения двойственной задачи записаны в виде уравнений.

Исходя из правила 7 запишем целевую функцию двойственной задачи:

.

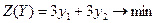Таким образом, двойственная пара будет иметь следующий вид:

Исходная задача:

,

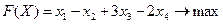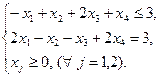
Двойственная задача:

.

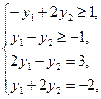
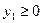Построенная двойственная пара является несимметричной.

Дата добавления: 2013-12-12