Возрастание и убывание функции

Производные высших порядков

Значения производной 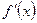зависят от 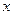, т.е. производная 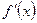представляет собой тоже функцию от 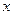. Дифференцируя эту функцию, мы получим вторую производную. Обозначается вторая производная следующим образом: 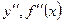. Аналогично получаются и производные третьего порядка 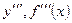и т.д.

В общем виде производная 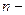го порядка от функции 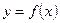называется производная (первого порядка) от производной 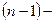го порядка и обозначаются символом 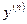. Записывается это следующим образом:

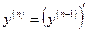(5.25)

При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется, монотонно возрастая, т. е. что каждое следующее ее значение больше предыдущего. Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.

Некоторые функции во всей своей области определения изменяются монотонно – только возрастают или только убывают. Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают.

Определение 5.7. Точка 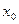называется точкой максимума (минимума) функции 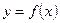, если в некоторой окрестности точки 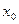выполняется неравенство .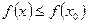

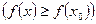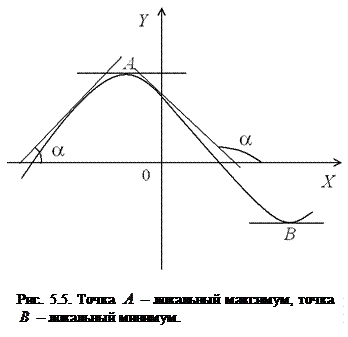
Следует иметь в виду, что максимум и минимум в данном случае являются локальными. На рис. 5.5 изображены локальные максимумы и минимумы. Максимум и минимум функции объединены общим названием: экстремум функции.

Из рис. 5.5. видно, что касательные, которые проходит через экстремумы функции параллельны оси абсцисс. Таким образом, угол между касательной и осью 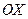равен нулю, а значит и производная равна нулю (поскольку 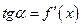). Кроме того, экстремумы функции могут наблюдаться и в тех точках, где производная не существует. Например, для функции 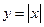в точке 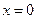(хотя левосторонняя и правосторонняя производная существуют, но они между собой не равны: , ).

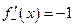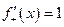Определение 5.8. Точки, в которых производная равна нулю, называются стационарными.

Определение 5.9. Точки, в которых производная равна нулю или не существует, называются критическими.

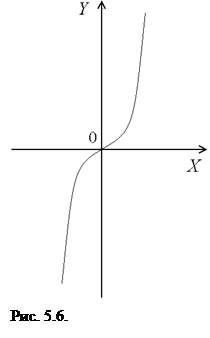
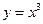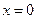Однако это вовсе не означает, что если данная точка является критической, то в ней обязательно будет наблюдаться либо максимум, либо минимум. Это необходимо, но не достаточно. Например, для функции точка является стационарной, однако в ней не наблюдается экстремума (см. рис. 5.6). Если функция возрастает в некотором интервале, то угол между касательной и осью абсцисс 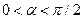, а значит тангенс и соответственно производная больше нуля. Если же функция убывает, то, очевидно, что 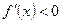. Таким образом, экстремумы обязательно наблюдаются в тех точка, при переходе через которые знак производной меняется на противоположный. Сформулируем теперь две теоремы, которые будут являться соответственно необходимым и достаточным условиями существования экстремума функции.

Теорема 5.1. (необходимый признак существования экстремума функции). Если дифференцируемая в точке 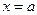функция 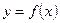имеет в этой точке максимум или минимум, то ее производная при 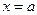обращается в нуль, .

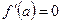Теорема 5.2. (достаточный признак существования экстремума функции). Если непрерывная функция 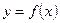имеет производную 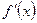во всех точках некоторого интервала, содержащего критическую точку 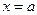(за исключением может быть самой этой точки), и если производная 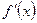при переходе аргумента слева направо через критическую точку 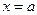меняет знак с плюса на минус, то функция в этой точке имеет максимум, а при переходе знака с минуса на плюс – минимум.

Дата добавления: 2013-12-12