Комбинаторика

Классическое определение вероятности событий

Основные понятия

СЛУЧАЙНЫЕ СОБЫТИЯ

ЛЕКЦИЯ №6

Контрольные вопросы

1. Сформулируйте понятие непрерывной функции в данной точке. 2. Сформулируйте понятие точки разрыва функции. 3. В чем принципиальное различие между точками разрыва первого и второго рода? 4. Сформулируйте понятие производной функции одной переменной. 5. Какая функция называется дифференцируемой в данной точке? 6. В чем состоит геометрический смысл производной? 7. Запишите правило дифференцирования суммы функций. 8. Запишите правило дифференцирования частного функций. 9. Запишите правило нахождения производной от произведения функций. 10. Сформулируйте правило дифференцирования сложных функций. 11. Сформулируйте понятие дифференциала функции одной переменной. 12. Возрастающая и убывающая функции. 13. Сформулируйте понятие точек максимумов и минимумов функции. 14. Запишите необходимый и достаточный признаки существования точек экстремумов функции.

План

1. Основные понятия.

2. Классическое определение вероятности событий.

3. Комбинаторика

4. Статистическая вероятность.

Окружающий нас мир пронизан явлениями, которые носят случайный характер. Мы встречаемся с ними, наблюдая состояние атмосферы, физические эксперименты, производственные процессы и т.п. Результаты многих наблюдений нельзя предсказать однозначно. Например, прогноз погоды на следующий день, курс доллара, количество дорожно-транспортных происшествий. Допустим, что, исходя из каких-то соображений, мы прогнозируем на завтра 11 дорожно-транспортных происшествий на улицах нашего города. Это событие может либо произойти, либо нет. Дело в том, что ситуация на дорогах зависит от большого количества факторов и учесть влияние каждого из них заранее невозможно (погода, видимость, направление и сила ветра, самочувствие водителей и пешеходов, количество и расположение транспорта на трассе и т.д.) Поэтому не исключено, что число происшествий окажется не 11, а, например, 10, 8, или 15. Рассмотренные события называются случайными. Раздел математики, изучающий случайные события называется теория вероятностей.

Время становления фундаментальных основ теории вероятностей относится к XVII веку. Вклад в формирование теории вероятностей внесли такие математики как Б. Паскаль (1623-1662), П. де Ферма (1601-1665), Галилей (1564-1642), Я. Бернулли (1654-1705) и др. В XIX веке теория вероятностей оформилась в стройную математическую теорию в связи с работами выдающихся русских ученых, таких как П. Л. Чебышев (1821-1894), А. А. Марков (1856-1922) и А. М. Ляпунов (1857-1918).

Основным понятием в теории вероятностей является случайное событие.

Определение 6.1. Случайным событием называется любой факт, который в условиях испытания может произойти или не произойти.

Под испытанием в этом определении подразумевается выполнение определенного комплекса условий. Далее вместо «случайного события» для краткости будем употреблять «событие».

События обозначаются прописными латинскими буквами: A, B, C, ….

Пример 6.1. Появление герба при подбрасывании монеты, выпадение осадков более 1000 мм в данном географическом пункте за определенный год – являются событиями.

События называются несовместными, если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными.

Пример 6.2. Несовместные события: выпадения цифры «5» при бросании игрального кубика исключает выпадение других цифр.

Пример 6.3. Совместные события: два стрелка стреляя по мишени, могут одновременно попасть по ней.

Событие называется достоверным 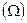, если в результате испытания оно обязательно должно произойти.

Событие называется невозможным 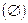, если в результате испытания оно не может произойти.

Пример 6.4. Извлечение белого шара из урны с белыми шарами – событие достоверное, а извлечение черного шара из той же урны – событие невозможное.

Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них.

Пример 6.5. Оценки «5», «4», «3», «2» – есть события единственно возможные по результатам курсового экзамена при наличии студента.

События называются равновозможными, если в результате испытаний по условиям симметрии ни одно из этих испытаний не является объективно более возможным.

Пример 6.6. Извлечение из полной колоды игральных карт дамы или короля – являются равновозможными.

Несколько событий образуют полную группу, если они являются единственно возможными и несовместными исходами испытаний. Два несовместных события, из которых одно должно обязательно произойти, называются противоположными.

Определение 6.2. Вероятность события – количественная мера неопределенности, число, которое выражает степень уверенности в наступлении этого события.

Проведем следующее испытание. Бросим один игральный кубик. В результате такого испытания возможны такие события: «выпала единица», «двойка», «тройка», «четверка», «пятерка» и «шестерка». Эти события, очевидно, образуют полную группу. Изобразим их совокупность в виде отдельных точек (см. рис. 6.1). Введем следующие определения. Единичный, отдельный исход испытания называется элементарным событием (элементарным исходом). Набор всех элементарных событий – множество элементарных исходов (пространство элементарных событий). Таким образом, любое событие можно рассматривать как подмножество пространства элементарных событий. Мы говорим, что событие произошло, если в результате испытания произошло элементарное событие, принадлежащее этому подмножеству. Например, нас интересует событие – выпало четное число. Этому событию соответствует набор (подмножество) трех элементарных событий – «двойка», «четверка» и «шестерка». Появление одного из этих элементарных событий будет означать, что произошло интересующее нас событие . Как в данном случае можно определить вероятность события? Очевидно, что чем выше удельный вес элементарных событий, соответствующих интересующему нас событию, тем больше шансов, что оно появится, т.е. тем выше вероятность. В нашем случае всего 6 элементарных исходов, из них 3 четных числа. Таким образом, вероятность будет равна .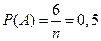

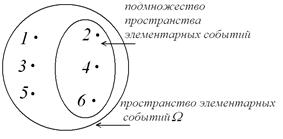
Рис. 6.1.

Рассмотренный метод является классическим, и сформировался в XVII веке в результате анализа азартных игр, и основано на понятии равновозможности событий.

Определение 6.3. Вероятностью наступления события называется отношение числа всех благоприятствующему этому событию элементарных исходов 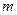к общему числу всевозможных простых, попарно несовместных, единственно возможных и равновозможных элементарных исходов испытания :

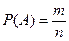(6.1)

Диапазон изменения вероятности случайного события: 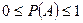. Вероятность достоверного события: 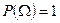. Вероятность невозможного события: 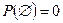. Чем больше значение вероятности, тем более мы уверены в наступлении события.

Приведем несколько примеров на нахождение вероятности наступления событий с использованием классического определения вероятности.

Пример 6.7. В урне 4 красных и 8 зеленых яблока. Случайным образом вынули одно яблоко. Найти вероятность того, что это яблоко – зеленое.

Решение:

Пусть событие заключается в появлении зеленого яблока. В данной задаче число всевозможных исходов 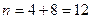, число исходов, которые благоприятствуют наступлению события 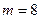. Тогда, согласно классическому определению вероятности:

.

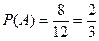Пример 6.8. Одновременно бросили два игральных кубика. Какова вероятность того, что на обеих гранях выпадет в сумме 8 очков?

Решение:

Пусть событие заключается в том, что при одновременном бросании двух кубиков выпадет число 8. Число всех возможных исходов , поскольку каждому значению на одном кубике может соответствовать 6 значений на другом 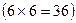. Для благоприятных исходов составим следующую таблицу:

Кубик №1
Кубик №2

Получили всего благоприятных исходов .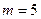

Вычисляем вероятность:

.

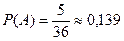Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. они в ряде случаев позволяют подсчитать количество всевозможных и количество благоприятных исходов.

Правило умножения в комбинаторике. Если первое действие можно осуществить 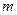различными способами, а второе – , то оба действия можно осуществить различными способами.

Это правило обобщается и на большее число действий. Например, если первое действие можно осуществить 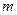различными способами, второе – , а третье 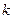, то все три действия можно осуществить 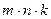различными способами.

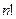Определение 6.4. Факториалом целого положительного числа (обозначается ) называется произведение первых чисел натурального ряда, т.е.:

(6.2)

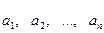Пусть имеется некоторое множество из элементов . Из этого множества можно образовать разные выборки, каждая из которых содержит 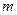элементов .

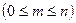Упорядоченные выборки называются размещениями.

Определение 6.5. Если комбинации из элементов по 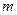отличаются либо составом элементов, либо порядком их расположения (либо и тем и другим), то такие комбинации называются размещениями из элементов по 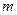. Число размещений из элементов по 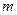равно:

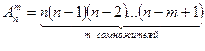(6.3)

или:

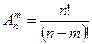(6.4)

Пример 6.9. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?

Решение:

Это есть число размещений:

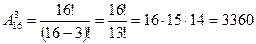
Определение 6.6. Если комбинации из элементов отличаются только порядком расположения этих элементов, то их называют перестановками из элементов. Число перестановок из элементов:

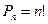(6.5)

Пример 6.10. Сколькими способами можно разместить 5 человек за столом, на котором поставлено 5 приборов?

Решение:

Это есть количество перестановок:

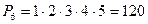
Определение 6.7. Если комбинации из элементов по 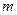отличаются только составом элементов, то их называют сочетаниями из элементов по 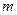. Число сочетаний изэлементов по :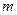

(6.6)

Пример 6.11. В хоккейном турнире участвуют 6 команд. Сколько матчей должно быть сыграно в турнире, если между любыми двумя командами должен быть сыгран только один матч?

Решение:

Каждый матч играется между двумя командами из 6 и отличаются только составом пар команд, т.е. представляют сочетание из 6 элементов по 2. Таким образом, находим:

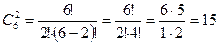
Пример 6.12. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность, что выбраны два мальчика? Выбор считать случайным.

Решение:

Событие состоит в том, что в члены делегации выбрали двоих мальчиков. Для решения этой задачи воспользуемся классическим определением вероятности, т.е.:

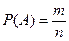
Число исходов, благоприятствующих наступления события равно:

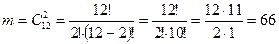
Число всех возможных исходов :

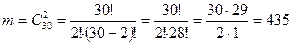
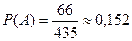
Определение 6.8. Если выбирать 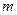элементов из , возвращая каждый выбранный элемент обратно, то такая выборка называется размещением из по 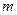с повторениями.

При этом 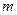и могут находиться в любом соотношени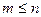и:

и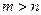

Общее количество 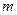выборок с возвращением равно:

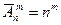(6.7)

Пример 6.13. Сколько различных трехзначных чисел можно составить из цифр 1, 2,3, 4, 5?

Решение:

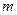Воспользуемся формулой (6.7). В данной задаче = 5, = 3.

.

Дата добавления: 2013-12-12