Способы образования выборки

Основные понятия

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

ЛЕКЦИЯ №10

Контрольные вопросы

1. Понятие числовых характеристик случайной величины. 2. Математическое ожидание для дискретной и непрерывной случайной величины. 3. Свойства математического ожидания. 4. Дисперсия для дискретной и непрерывной случайной величины. 5. Свойства дисперсии. 6. Среднеквадратическое отклонение. 7. Нормальное распределение случайной величины. 8. Свойства нормального распределения. 9. Стандартный нормальный закон распределения. 10. Как рассчитать вероятность попадания случайной величины, распределенной по нормальному закону в данный интервал?

План

1. Основные понятия

2. Способы образования выборки

3. Вариационный ряд

4. Понятие числовых характеристик

Термин статистика употребляется чаще всего для обозначения двух понятий. Во-первых, статистикой называют набор количественных данных о некотором явлении, совокупности объектов и т.п. Например, каждую студенческую группу можно охарактеризовать так: в ней всего студентов, из которых 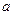отличников, 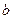хорошистов, троечников, неуспевающих. Во-вторых, термином статистика объединяют совокупность методов, основанных на анализе статистических данных. Например, данные о среднем доходе граждан собирают ежемесячно в течение года, затем делают вывод о том, как изменялся уровень жизни различных слоев населения.

В каждой области деятельности разработаны свои специфические статистические методы. Существует много разных статистик: социально-экономическая, демографическая, юридическая и т.п. Цели статистического наблюдения в юриспруденции могут быть самыми разными. Они вытекают из реальных социально-правовых потребностей правоохранительных и других юридических учреждений или государства в целом. Например, отслеживание уровня учтенной преступности, раскрываемости, судимости и общего числа заключенных составляет базу данных, на основе которой организуется борьба с преступностью и оценивается безопасность общества.

Поскольку всякая статистика оперирует с числами, то основой всех статистических методов является математика. Совокупность математических методов обработки, систематизации, анализа и использования статистических данных составляет предмет специальной науки – математической статистики.

Две основные задачи математической статистики:

1) Указать способы сбора и группировки сведений, полученных в результате наблюдений или в результате поставленных экспериментов.

2) Разработка методов анализа полученных данных в зависимости от целей исследования.

Таким образом, основная задача математической статистики в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Статистика изучает совокупности однородных, в некотором роде, объектов, относительно некоторого качественного или количественного признака.

Определение 10.1. Совокупность всех объектов подчиненных данному признаку, называется генеральной совокупностью.

Обычно из всей совокупности выбирают ограниченное число объектов, которые подвергают изучению. Такую случайно отобранную совокупность называют выборочной совокупностью или выборкой.

Определение 10.2. Объемом совокупности (выборочной или генеральной) называется число объектов этой совокупности.

Определение 10.3. Подборка, достаточно хорошо описывающая всю генеральную совокупность, называется репрезентативной (представительной).

Для получения репрезентативной выборки необходимо, чтобы все отобранные элементы имели одинаковую вероятность попадания в выборку. В случае большого объема генеральной совокупности применяются датчики случайных чисел (таблицы, ЭВМ и другие).

Преимуществами выборочного метода наблюдения по сравнению со сплошным является: экономия всех видов ресурсов, снижение ошибок регистрации (расхождения между истинными и зарегистрированным значениями признака); незаменимость в случае, когда исследование связано с уничтожением наблюдаемых объектов.

Основной недостаток выборочного метода – ошибки репрезентативности, возникающие только за счет того, что исследуется не вся совокупность, а лишь выборка из нее. Ошибки репрезентативности могут быть случайными и систематическими. Случайные ошибки возникают из-за того, что совокупность отобранных единиц наблюдения неполно воспроизводит всю совокупность в целом. Систематические ошибки возникают вследствие нарушения принципов случайного отбора единиц изучаемой совокупности.

Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. Такая выборка называется собственно-случайной.

Используют два способа образования выборки:

1. Отбор, не требующий разбиения генеральной совокупности на части. Сюда относятся:

— простой случайный бесповторный отбор;

— простой случайный повторный отбор.

2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:

— типический отбор;

— механический отбор;

— серийный отбор.

Повторный отбор – когда каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран.

Бесповторный отбор – когда отобранный элемент не возвращается в общую совокупность.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части. Например, если продукция изготовляется на нескольких машинах, среди которых есть более и менее изношенные, то такой отбор становится целесообразным.

Механический отбор – отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных на станке деталей, то отбираю каждую пятую деталь; если 5%, то отбирают каждую двадцатую и т.д.

Серийным называют отбор, при котором объекты отбирают не по одному, а «сериями», которые подвергаются сплошному обследованию. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.

Отметим, что на практике применяется часто комбинированный отбор, при котором сочетаются указанные выше способы.

Дата добавления: 2013-12-12