Замечания

1. Момент импульса системы может сохраняться при наличии внешних сил при условии взаимной компенсации их моментов.

2. Момент импульса системы может сохраняться если действует внешняя центральная сила, а полюс О выбран в центре силового поля.

3. Для произвольной механической системы закон сохранения момента импульса не удается получить простым обобщением закона сохранения момента импульса для материальной точки, т. к. нельзя провести преобразования аналогичные преобразованиям, переводящим (2.22) в (2.31). Это связано с тем, что, в отличие от аддитивных величин, таких, как момент импульса системы L, момент внешних сил M и момент инерции, угловые скорость w и ускорение e не аддитивны и для различных элементов системы могут иметь различные значения, и для системы, как единого целого, не определены.

6.3. Закон сохранения механической энергии

Если на материальную точку (тело) действует сила, то ее (его) кинетическая энергия не остается постоянной. Интегрируя соотношение (5.12), получим, что

.

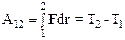Физический смысл полученной формулы

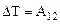
заключается в следующем:

· приращение кинетической энергии материальной точки равно работе равнодействующей сил, приложенных к ней.

6.3.1. Механическая энергия материальной точки

(тела) под воздействием консервативной силы

Работа консервативной силы при перемещении материальной точки (тела) из положения 1 в положение 2 – А₁₂ может быть представлена (см. (5.1)) как убыль потенциальной энергии

.

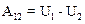Соотношение (6.4), в свою очередь, указывает, что в результате совершения работы увеличивается кинетическая энергия. Сравнивая (5.1) и (6.4) приходим к выводу, что:

,

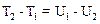или собирая члены, соответствующие одному состоянию в различных частях уравнения:

.

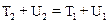Полученный результат означает, что величина полной механической энергии частицы (тела) E=T+U для в поле консервативных сил остается постоянной.

· При отсутствии неконсервативных сил полная механическая энергия остается постоянной – сохраняется.

· Увеличение кинетической энергии системы в присутствии консервативных сил происходит за счет убыли ее потенциальной энергии. Наоборот, уменьшению кинетической энергии системы в присутствии консервативных сил соответствует увеличение ее потенциальной энергии.

6.3.2. Механическая энергия материальной точки

(тела) под воздействием произвольных сил

В общем случае на материальную точку (тело) могут действовать силы консервативные F и неконсервативные F *. В этом случае (см. (4.4)) полная работа А₁₂ при перемещении из положения 1 в положение 2 равна сумме работ консервативных и неконсервативных сил

.

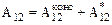Как известно (5.1), работа консервативных сил равна убыли потенциальной энергии, и соотношение (6.5) можно переписать так

.

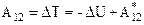Преобразуем полученное выражение

,

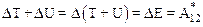здесь E=T+U, как всегда, – полная механическая энергия. Полученный результат означает, что

· работа неконсервативных сил затрачивается на изменение полной механической энергии.

При условии, что кинетическая энергия в начальном и конечном положениях системы одна и та же, работа неконсервативных сил идет на изменение потенциальной энергии.

6.3.3. Механическая энергия системы

A. Рассмотрим механическую систему, состоящую из n невзаимодействующих частиц, находящуюся в поле консервативных сил. Каждая из этих частиц обладает потенциальной U_i и кинетической T_i энергией. Для каждой частицы системы справедливо утверждение

.

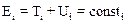Суммируя эти равенства по всем частицам получим

.

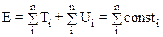Соотношение (6.11) показывает, что полная механическая энергия системы невзаимодействующих между собой частиц в поле консервативных сил является аддитивной величиной. Наконец, из него следует закон сохранения энергии:

· полная механическая энергия системы невзаимодействующих между собой частиц, на которые действуют только консервативные силы, остается постоянной.

B. Рассмотрим, теперь, механическую систему, состоящую из n частиц, на которые могут действовать как консервативные F, так и неконсервативные F * силы. Каждая из этих частиц обладает потенциальной U_i и кинетической T_i энергией. Для i-ой частицы такой системы справедливо утверждение (6.9): при переходе из состояния 1 в состояние 2 изменение полной механической энергии этой частицы равно работе неконсервативных сил:

,

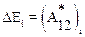здесь 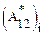– работа неконсервативной силы, действующей на i-ю частицу.

Суммируя аналогичные равенства для всех частиц системы получим

.

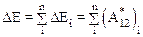С. Рассмотрим, наконец, общий случай механической системы, состоящей из n взаимодействующих между собой частиц. Предположим, что величина внутренних сил f _ij зависит только от взаимного расстояния между частицами. Такие силы являются консервативными. Предположим также, что на частицы системы действуют внешние консервативные F _iи внешние неконсервативные F _i* силы.

Уравнение второго закона Ньютона для i-ой частицы имеет вид:

.

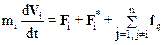Умножая это уравнение скалярно на элементарное перемещение частицы d r _i= V _idt, получим

.

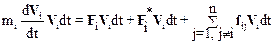Если записать аналогичные уравнения для всех частиц системы и сложить их, то придем к выражению

.

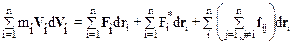Выясним смысл всех членов уравнения (6.13). Левая часть уравнения 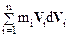в соответствии с (5.12) представляет собой приращение dT кинетической энергии системы. Член 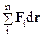согласно (5.1) равен убыли потенциальной энергии –dU_внешн системы во внешнем поле. Член 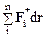равен работе 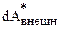внешних неконсервативных сил. Наконец, как следует из соотношений (4.4), (5.1), последний член в (6.13) 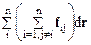равен убыли потенциальной энергии –dU_вз взаимодействия частиц. Таким образом, формулу (6.13) можно записать так:

,

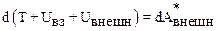где 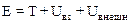– полная механическая энергия системы. Соотношение (6.14) позволяет дать следующую формулировку закона сохранения энергии:

· полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.

Обратимся вновь к формуле (6.14), которая показывает, что механическая энергия системы может измениться только за счет работы неконсервативных сил. Это замечание позволяет дать еще одну формулировку закона сохранения энергии:

· если отсутствуют неконсервативные силы или они таковы, что не совершают работы в течение некоторого промежутка времени, то полная механическая энергия системы, находящейся в стационарном поле консервативных сил, остается постоянной в течение этого промежутка времени.

Уравнения (6.6), (6.11) и (6.14) это различные выражения закона сохранения полной механической энергии системы.

6.3.4. Упругое столкновение

· Абсолютноупругим называют столкновение тел, которое не сопровождается изменением их внутреннего состояния. В ходе абсолютно упругого столкновения происходят превращения механической кинетической энергии движущихся тел в потенциальную энергию и наоборот. При упругом ударе тела деформируются (сплющиваются), их кинетическая энергия частично переходит в потенциальную энергию упругих деформаций. Под действием возникших сил упругости тела стремятся перейти в недеформированное состояние. При этом энергия деформации вновь переходит в энергию поступательного движения, и тела разлетаются в разные стороны.

Таким образом, при анализе процесса упругого столкновения достаточно рассмотреть механическую энергию сталкивающихся тел.

· Центральныйудар – удар, при котором тела до удара движутся вдоль линии, соединяющей их центры масс.

Рассмотрим абсолютно упругий центральный удар двух шаров, имеющих массы m₁ и m₂ и движущихся поступательно (без вращения) со скоростями V ₁₀ и V ₂₀. Обозначим через V ₁ и V ₂ скорости первого и второго шаров после столкновения. Как отмечено выше, в процессе столкновения выполняется закон сохранения механической энергии:

.

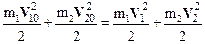Если промежуток времени до удара и после него стремится к нулю, то применим также закон сохранения импульса системы:

.

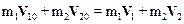Соотношения (615) и (6.16) удовлетворяются одновременно, и образуют систему уравнений:

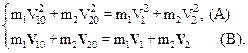
Решая систему (6.17) найдем скорости, которые приобретают шары в результате столкновения. Заметим, что очевидным тривиальным решением системы является решение вида:

V ₁₀= V ₁ и V ₂₀= V ₂.

Физически такое решение означает, что скорости шаров не изменились, а, значит, их столкновение не произошло. Будем считать, что V ₁₀¹ V ₁ и V ₂₀¹ V ₂. Это замечание позволяет преобразовать уравнения системы следующим образом:

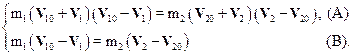
Разделив почленно уравнения системы, имеем:

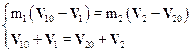
Если умножить второе уравнение системы (6.19) на m₂ и вычесть его из первого, то после преобразований получим для скорости V ₁ первого шара:

.

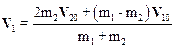Умножив второе уравнение системы (6.19) на m₁ и сложив со вторым, получим:

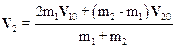
Дата добавления: 2013-12-12