Динамика специальной теории относительности

10.2.1. Релятивистский импульс

Классическое выражение для импульса частицы массой m

.

не инвариантно относительно преобразований Лоренца. Учитывая, что при малых скоростях собственное время частицы dt (время по часам, движущегося вместе с частицей) близко ко времени dt, измеренному по часам в неподвижной системе отчета, т. е. .

Запишем выражение для импульса (10.37) следующим образом:

,

где d r – вектор перемещения частицы.

Проверим инвариантность определения (10.37) по отношению к преобразованиям Лоренца. Рассмотрим процесс абсолютно упругого столкновения частиц с массами m₁ и m₂ в системах К и К¢, предполагая, что закон сохранения импульса справедлив в системе отсчета К. Запишем уравнение закона сохранения импульса:

,

здесь правая часть равенства представляет собой полный импульс системы частиц до столкновения, левая – после столкновения.

Проецируя соотношение (10.38) на оси x, y, z. Получаем:

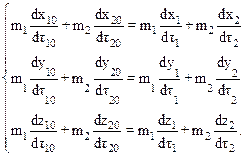
Перейдем к системе К¢, имея в виду что собственное время dt – инвариантно:

Проекции перемещений d r ₁₀ и d r ₂₀ в направлении оси x испытают лоренцево сокращение, в направлении осей y и z не изменятся:

.

Разделим первое равенство системы (10.39) на . Учитывая соотношения (10.40) и (10.41), получим:

Возвращаясь к векторной записи, имеем:

.

Таким образом, выражение для импульса (10.37) оказывается инвариантным относительно преобразований Лоренца, и, соответственно, закон сохранения импульса в СТО выполняется.

Так как собственное время частицы связано с временем t в системе К, относительно которой наблюдается движение тела, то для импульса в системе К получим:

.

Очевидно, что при V<<c соотношение (10.43) переходит в выражение для классического импульса P =m V. Иногда формулу (10.43) трактуют иначе: импульс, как в классической механике Ньютона, определяются выражением P =m V, но массутела считают не инвариантной величиной, а зависящей от скорости:

.

Масса m_r, определяемая соотношением (10.44) называется релятивистской массой; инвариантной массой является m₀ – масса покоя. Таким образом, релятивистский импульс принято записывать так:

.

10.2.2. Основное уравнение динамики СТО

Основное уравнение динамики тела с массой m – уравнение второго закона Ньютона:

.

Если для импульса частицы использовать релятивистское выражение (10.45), то подстановка его в (1.46) дает выражение, инвариантное относительно преобразований Лоренца:

.

Уравнение (10.47) называют основным уравнением динамики СТО.

10.2.3. Релятивистское выражение для энергии

Умножим обе части (10.47) на перемещение частицы d r = V dt:

.

Правая часть (10.48) равна элементарной работе dA силы F на перемещении d r. По закону сохранения энергии эта работа идет на увеличение полной энергии частицы:

F d s = dE.

следовательно:

.

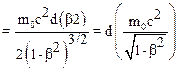Таким образом, приходим к соотношению:

.

Интегрируя обе части (10.48), получим:

.

Соотношение (10.49) оказывается инвариантным по отношению к преобразованиям Лоренца, если постоянная интегрирования равна нулю.

Итак:

.

При V=0 соотношение (10.50) принимает вид:

,

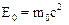где использовано обозначение E₀ для неподвижного тела. Эту энергию называют энергиейпокоя или собственной энергией тела. Энергия покоя – это внутренняя энергия, не связанная с перемещением тела в пространстве как целого и/или его положением во внешнем потенциальном поле. В нее входит потенциальная энергия взаимодействия частиц тела между собой и кинетическая энергия движения этих частиц около общего центра масс.

Кинетическую энергию тела определяют как разность полной релятивистской энергии (10.50) и энергии покоя (10.51):

.

При малых скоростях (b®0), можно, используя приближенную формулу

,

где х=b² привести соотношение (10.53) к обычному виду классической механики Ньютона:

Сравнивая (10.50) с выражением для импульса (10.43), получим:

.

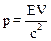10.2.4. Взаимосвязь массы и энергии

Воспользуемся релятивистским соотношением (10.51) для полной энергии частицы массой m, движущейся со скоростью V:

,

или выражением (10.44) использующим понятие релятивистской массы:

.

Очевидно, что энергия и релятивистская масса пропорциональны друг другу; соотношение (10.54) устанавливает эквивалентностьмассы и энергии. Из этого же соотношения следует:

.

Физический смысл выражения (10.56) состоит в следующем:

изменение релятивистской энергии (кроме энергии во внешнем поле) влечет изменение релятивистской массы тела:

.

10.2.5. Связь между энергией и импульсом тела

Дата добавления: 2013-12-12