Лекция 1 механика. Часть I

КОНСПЕКТ ЛЕКЦИЙ

Часть I

ФИЗИКА

Подписано к печати		Формат 60 ´ 84/16
Тираж 300 экз.		Заказ №	Усл. п. л.

127994 Москва, А-55, ул. Образцова д. 9, стр.9. Типография МИИТ

ПРЕДИСЛОВИЕ

Настоящее пособие является конспектом курса лекций, которые автор читает в первом семестре курса физики студентам МИИТа (весь курс рассчитан на три семестра). Обычно учебные планы рассчитываются, исходя из предположения о том, что в каждом семестре будут прочитаны 18 лекций. Однако по различным причинам (к которым относятся праздники, разного рода мероприятия, требующие присутствия на них студентов-первокурсников и т. д.) реальное число лекций за семестр оказывается меньшим. Именно поэтому данный конспект составлен, исходя из предположения, что лекций удаётся прочитать только 17. Впрочем, во введении ко всему конспекту, а также в качестве примеров проявления тех или иных физических эффектов по теме каждой лекции в пособии приведён материал, который может быть использован преподавателем в аудитории в том случае, если потерь в лекционных часах не происходит.

При нехватке лекционного времени часть материала может быть опущена (например, введение, раздел 12.2 и т. д.).

Конспект не заменяет учебники, рекомендуемые для изучения общей физики; он лишь призван служить дополнительным источником информации, облегчающим освоение студентами этого курса. К числу основных учебников и задачников, используемых в МИИТе, относятся следующие:

1. Детлаф А.А., Яворский Б.М. Курс физики: Учеб. пособие для втузов. – М.: Высш. школа, 2002. – 718 с.

2. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – М.: Высш. школа, 2004. – 544 с.

3. Савельев И.В. Курс общей физики в 3-х тт. – М.: Астрель АСТ, 2007.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Наука, 1985 - 2004.

5. Чертов А.Г., Воробьёв А.А. Задачник по физике: Учеб. пособие для вузов. – М.: Изд. Физ.-мат. литературы, 2002. – 640 с.

6. Сборник задач по дисциплине «Физика» / Под общ. ред. проф. С.М. Кокина – М.: МИИТ, 2006. – 144 с.

ВВЕДЕНИЕ

· Наука и научное знание

На протяжении всей своей истории люди выработали разные способы познания и освоения окружающего их мира, и одним из них является наука. Сам термин «наука» – Science – происходит от латинского слова Scientia (знание). Однако не всякое знание является наукой! Дело в том, что кроме науки по-своему отражают реальность, формируют свои области знаний, например, ещё искусство и религия. Но лишь наука создаёт мир знаний, состоящий лишь из экспериментально доказанных данных об этом мире и выводов, полученных на основе законов логики. В этом мире самому человеку, его субъективным оценкам, предпочтениям отводится весьма незначительная роль.

Когда говорят о научном методе познания, то подразумевается, что этот метод основан на следующих принципах:

1. Принцип причинности. «Ни одна вещь не возникает беспричинно, но всё возникает на каком-нибудь основании и в силу необходимости», – Демокрит (около 460 – 370 гг. до н. э.). Сказанное означает, что в основе любого следствия всегда должна лежать некоторая причина (возникшее следствие, в свою очередь, может повлиять на причину). Этот принцип имеет объективный и всеобщий характер, и именно поэтому на нём базируется вся материально-техническая деятельность человека.

2. Принцип воспроизводимости результатов. Естественнонаучная истина проверяется (доказывается) только практикой: наблюдениями, опытами, производственной деятельностью. «Наука началась тогда, когда люди научились мерить; точная наука немыслима без меры», – Д.И. Менделеев (1834 – 1907). Однако говорить о научной истине можно лишь в том случае, если результаты исследований воспроизводимы. Это означает, во первых, что полученный однажды результат должен допускать его повторение независимыми исследователями. Во-вторых, этот критерий выносит в разряд ненаучных такие невоспроизводимые явления, как, например, НЛО. Конечно, по поводу невоспроизводимых явлений можно строить различного рода предположения, отыскивать подтверждения их справедливости, однако даже после получения серии доказательств, говорящих в их пользу, всегда будет оставаться место для сомнений: нельзя ли тот же результат объяснить по иному? В связи с этим следует вспомнить принцип, предложенный английским философом У. Оккамом (около 1300 – 1350): для объяснения чего-либо «не следует умножать сущности без надобности», то есть не нужно выдумывать новых гипотез, если это «что-то» можно объяснить, исходя из уже известных представлений.

С принципом воспроизводимости результатов тесно связан приведённый выше основной признак, который отличает науку от других способов познания окружающего мира: любая гипотеза должна подвергаться проверке экспериментом (не зря научная гипотеза определяется, как научное предположение, требующее проверки на опыте и теоретического обоснования). Пусть в пользу некоторой гипотезы говорит множество фактов, однако достаточно появиться только одному, который её опровергает, гипотезу придётся пересматривать. Так, например, весь массив накопленных наукой экспериментальных данных говорил в пользу справедливости законов классической механики, однако, в конце XIX – начале XX веков появились результаты новых исследований, и оказалось, что эти законы имеют приближённый характер: была создана специальная теория относительности (А. Эйнштейн, 1879 – 1955).

3. Принцип возможности предсказания новых явлений и эффектов. В основу научной теории гипотеза ложится лишь в том случае, если на её основе удаётся сделать предсказания новых явлений и эффектов, таких, которые, опять-таки допускают экспериментальную проверку, но которые не могут быть объяснены другими гипотезами.

4. Принцип относительности научного знания. Научные понятия, идеи, концепции, модели, теории, выводы из них всегда относительны и ограничены. Задача учёного – установить границы соответствия существующего научного знания действительности. Здесь, во-первых, следует помнить, любой эксперимент характеризуется ошибками измерения (погрешностью). Совершенствование процедуры измерений позволяет уменьшить эти ошибки, однако, как ни совершенствуй измерительную аппаратуру, соответствующие погрешности хоть и могут стать меньше, но всё же окончательно не исчезнут, поскольку любой прибор характеризуется вполне определёнными диапазоном измерений и чувствительностью.

Во-вторых, существование погрешностей зачастую оказывается принципиально связано с той методикой, с теми теоретическими представлениями, которые положены в основу процедуры измерения. Так, например, долгое время казалось, что по мере совершенствования оптических приборов будут создаваться всё более и более мощные микроскопы, которые, в идеале должны дать возможность измерить размеры отдельных молекулы и атомов. Но этого не произошло из-за того, что для столь малых объектов наблюдения, сами принципы геометрической оптики оказываются неприменимыми. Чем меньше объект, тем более существенной становится необходимость учёта волновых свойств электромагнитного излучения: свет огибает этот объект (явление дифракции), и поэтому увидеть последний оказывается невозможно.

К методам научного познания в настоящее время относят: наблюдение, измерение, индукцию, дедукцию, анализ, синтез, абстрагирование, моделирование и эксперимент.

· Описание окружающего мира. Явления и эффекты. Определения. Единицы измерения физических величин. Законы

Понять окружающий мир, это, прежде всего, – описать его. В свою очередь, описание начинается с выявления в природе, в различных областях практической деятельности человека причинно-связанных событий: эффектов и явлений, объяснение которым и даёт наука. Перечислим некоторые из подобных физических явлений:

- Термоэлектронная эмиссия – явление испускания электронов нагретыми металлами и полупроводниками;

- Интерференция – явление возникновения устойчивой во времени картины распределения максимумов и минимумов колебаний при наложении друг на друга нескольких волн;

- Радиоактивный распад – явление распада ядер атомов на более лёгкие ядра и элементарные частицы.

Важным этапом описания наблюдаемого эффекта является введение общепринятых терминов, определений, оперируя которыми можно однозначно информировать окружающих о результатах исследований. В каждой области человеческой деятельности есть свои термины и определения. Приведём примеры определений, используемых в физике (а также в разных областях техники): путь, перемещение, ускорение, импульс, работа, давление, потенциал, эдс, магнитный поток, индуктивность и т.д. Знакомство с любой новой отраслью знаний, – это, прежде всего, освоение используемой в этой отрасли системой терминов и определений, и физика здесь не является исключением.

Количественное соотношение между параметрами, вводимыми а основе определений, невозможно без установления системы единиц измерения величин этих параметров. Часть из этих единиц принимаются за основные (по договорённости для их определения выбираются эталоны), оставшиеся являются производными, определяемыми через основные (хотя производные единицы зачастую и имеют собственное название).

В широко распространённой в настоящее время международной системе единиц СИ основных единиц семь:

- метр – единица измерения длины (м);

- секунда – единица измерения времени (с);

- килограмм – единица измерения массы (кг);

- кельвин – единица измерения температуры (К);

- моль – единица измерения количества вещества (моль);

- ампер – единица измерения силы тока (А);

- кандела – единица измерения силы света (кд).

Примеры производных единиц с указанием того, что в них измеряется: метр в секунду (м/с) – скорость; метр в секунду за секунду, (м/с²) – ускорение; килограмм на метр в секунду (кг×м/с) – импульс.

Примеры производных единиц, которые имеют в СИ собственное название, с указанием того, что в них измеряется и общепринятыми обозначениями соответствующих параметров:

- ньютон – сила F; 1 Н = 1 кг×м×с^-2;

- джоуль – работа A, энергия E, W, количество теплоты Q;

1 Дж = 1 Н×м = 1 кг×м²×с^-2;

- ватт – мощность N, P; 1 Вт = 1 Дж×с^-1 = 1 кг×м²×с^-3;

- паскаль – давление p; 1 Па = 1 Н×м^-2 = 1 кг×м^-1×с²;

- кулон – заряд q; 1 Кл = 1 А×с;

- вольт – потенциал j, напряжение U, э. д. с. E;

1 В = 1 Дж/Кл = 1 кг×А^-1×м²×с^-3;

- фарад – электроёмкость C; 1 Ф = 1 Кл/В = 1 А²×с⁴×кг^-1×м^-2;

- ом – электрическое сопротивление R, r;

1 Ом = 1 В/А = 1 кг×м²×с^-3×А^-2;

- тесла – индукция магнитного поля B;

1 Тл = 1 Н/(А×м) = 1 кг×А^-1×с^-2;

- вебер – магнитный поток F; 1 Вб = 1 Тл×м² = 1 кг× м²×А^-1×с^-2;

- генри – индуктивность L; 1 Гн = 1 Вб/А = 1 кг× м²×А^-2×с^-2;

(Напомним, сокращения единиц измерения, названных так в честь известных учёных, пишутся с большой буквы).

На основании экспериментальных данных и теоретических построений, призванных объяснить эти данные, удаётся устанавливать определённые законы. Для количественного отображения связи между соответствующими физическими величинами используются формулы, однако следует помнить, что далеко не всегда записанная формула полностью отображает суть закона. Так, например, формулу для силы Ампера, которая действует на проводник с током, помещённый в магнитное поле, можно записать в виде:

F _А = B×I×l×sin a.

Однако, во-первых, следует объяснить, что имеется в виду под символами F _А, I, l, B и о каком угле a идёт речь, но и, во-вторых, необходимо сказать, как определяется направление действия этой силы.

Заметим, многие из переменных, входящих в формулы физических законов, являются векторами, и об этом нельзя забывать. Так, запись формулы для силы Ампера в векторном виде выглядит следующим образом:

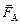= I ×[]

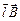(здесь квадратными скобками обозначено векторное произведение векторов 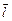и 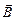: понятно, что, используя эту формулу, нужно знать, как выбирается направление этих векторов).

Сталкиваясь с конкретной практической ситуацией, исследователь прежде всего создаёт её упрощенную модель, отражающую основные особенности ситуации. Примерами моделей являются материальная точка, нерастяжимая нить, абсолютно твёрдое тело, идеальный газ, точечный заряд и др. Чем проще модель, тем легче описать её математически. Именно это и имеет место в учебных задачах, которые приведены в стандартных задачниках по физике. В большинстве случаев там сразу понятно, о каких явлениях, эффектах идёт речь, какие законы соответствуют этим явлениям, и какие, описывающие эти законы формулы, должны быть привлечены для решения задачи. В реальности, однако, зачастую неизвестно, какие из параметров являются существенными, а какие – нет, и только эксперимент подскажет, правильно ли вы рассчитали результат, или он далёк от истины. Но только решая учебные задачи можно научиться «чувствовать ситуацию», овладеть навыками самостоятельной работы, то есть – стать грамотным специалистом.

1.1 КИНЕМАТИКА

1.1.1 Основные понятия

1.1.2 Равномерное движение по прямой

1.1.3 Равнопеременное движение по прямой

1.1.4 Движение вдоль прямой с переменным ускорением

1.1.5 Движение тела, брошенного под углом к горизонту

1.1.6 Движение точки по окружности

Некоторые примеры

Вопросы для повторения

1.1 КИНЕМАТИКА

1.1.1 Основные понятия

Кинематика – раздел физики, в котором решается основная практическая задача, возникающая перед человеком: где окажется движущееся тело в заданный момент времени. Снаряд вылетел из пушки: попадёт в цель или нет? Отправляем корабль: сколько времени понадобится для достижения конца пути? Провожаем поезд: где он окажется через заданный промежуток времени? При этом то, почему происходит движение, что и по какой причине влияет на движущийся объект, в кинематике не обсуждается.

Для решения поставленной задачи, то есть для описания движения тела используется математика.

Как говорилось во введении, прежде, чем начать такое описание, следует ввести серию определений (большая часть из которых должна быть достаточно хорошо известна из школьного курса физики).

Траекторией называется мысленно проведённая в пространстве линия, соединяющая последовательно все точки, в которых побывало (или может побывать) тело в процессе движения. Линия может быть отрезком прямой, окружностью, параболой, спиралью и т. д., при этом любая линия характеризуется вполне определённым численным параметром: своей длиной. Тело пока будем считать точечным объектом, размеры которого много меньше данной длины.

Путь – это длина траектории (скалярная величина, которая не бывает отрицательной); в СИ измеряется в метрах (или кратных метру единицах: мм, км и т. д.). Из определения следует, что если в какой-то задаче требуется рассчитать путь, пройденный телом, сначала следует представить себе (нарисовать) траекторию его движения, линию, длину которой и нужно будет найти. Линия может состоять из участков разной формы, длину каждого из которых в этом случае придётся рассчитывать отдельно.

Перемещением 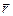называется вектор, проведённый из начальной точки траектории в любую другую заданную точку (например, – в конечную).

В отличие от пути (параметра, не позволяющего сказать, куда двигалось тело), перемещение даёт возможность определить конечное положение тела в пространстве. Действительно, ели выбрать систему координат, например, декартову прямоугольную с осями 0X, 0Y, 0Z, начало которой совпадает с началом траектории (рис. 1.1), вектор перемещения окажется радиусом-вектором конечной точки траектории, координаты которой можно обозначить x, у и z. В этом случае основная задача кинематики сведётся к вычислению x, у и z в интересующий нас момент времени t. Заметим: |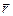| = 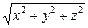, и если тело движется по прямой, систему координат удобно выбирать так, чтобы одна из осей (0X) была направлена вдоль данной прямой. В этом случае проекции вектора перемещения на оси 0Y и 0Z будут равны нулю, а |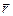| = || = 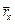x.

Следующее определение – скорость тела.

Вообще говоря, в математике скоростью изменения какой-либо функции f называется первая производная этой функции по времени 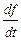(другое обозначение производной по времени, используемое со времён Ньютона, – точка над символом функции: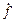; заметим: производную по координате принято обозначать, не точкой, а штрихом – 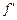, указывая, если нужно, по какой из координат идёт дифференцирование: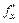, , 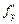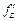). 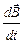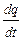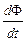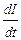Так, можно говорить, что, например, , , и – скорости изменения магнитной индукции; заряда; магнитного потока и силы тока соответственно.

В механике скоростью 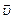(иногда такую скорость называют мгновенной) называется первая производная по времени от вектора 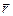перемещения (единица измерения в СИ – м × с ^-1):

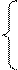u_х =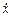

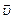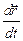= , или u_y = 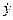(1.1)

u_z = .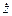

Очевидно, что при движении вдоль оси координат 0X

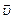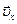|| = || º u_х =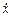

Ускорением называется первая производная по времени от вектора 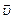скорости (скорость изменения скорости):

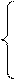а_х =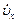

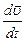= , или а_y = 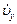(1.2)

а_z = .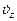

При движении вдоль оси 0X

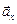|| = || º a_х = =.

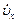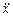В СИ ускорение измеряется в м × с ^-2.

Рассмотрим простейшую ситуацию – движение тела по прямой. Заметим: даже самую сложную траекторию можно представить в виде совокупности некоторого (пусть даже большого) числа прямолинейных участков[1], для каждого из которых можно записать приводимые ниже формулы. Продемонстрируем, как «работают» введённая нами система определений плюс математика.

1.1.2 Равномерное движение по прямой

Равномерным называется движение, при котором выполняется условие

(1.6)

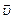= const. (1.3)

Из определений (1.1) ¸ (1.3) следуют несколько выводов.

- Условие (1.3) означает постоянство вектора скорости как по величине, так и по направлению, то есть его выполнение означает, что тело движется по прямой.

- Так как производная от константы равна нулю, то – см. определение (1.2) – при равномерном прямолинейном движении тело не имеет ускорения (= 0).

- Выбрав ось координат 0X вдоль направления движения тела, можно записать: u =, или

dx = udt.

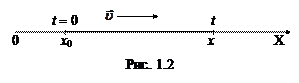Найдем закон, по которому координата тела x меняется со временем t (то есть решим основную задачу кинематики).

Пусть тело в момент времени t = 0 находилось в точке с координатой х ₀. Тогда

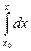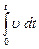= , или (так как u = const): 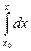= u ,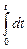

x - x ₀= ut.

Таким образом, при равномерном движении тела по прямой его координата должна меняться со временем по известному из школьной программы закону:

x = x ₀ + ut. (1.4)

Знаки «плюс» перед x ₀ и u говорят о том, что при выбранных направлении оси 0X и месте нахождения начала отчёта (точки 0) координата x ₀ и проекция скорости 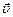на ось 0X положительны.

1.1.3 Равнопеременное движение по прямой

Равнопеременным называется движение, при котором выполняется условие

= const. (1.5)

При этом если вектора скорости и ускорения параллельны ( ↑↑ 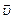), то такое движение называется равноускоренным: за одинаковые промежутки времени скорость тела увеличивается на одну и ту же величину.

Если вектора 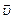и ускорения антипараллельны ( ↑↓ ), то такое движение называется равнозамедленным: за одинаковые промежутки времени скорость тела уменьшается на одну и ту же величину.

Использование определения (1.5) позволяет вывести зависимости скорости u от времени t при равноускоренном движении. Так, выбрав ось координат вдоль направления движения тела (рис 1.3), можно записать: а =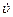, или du = аdt. Если тело в момент времени t = 0 тело имело скорость u ₀, то

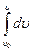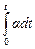= , или (так как а = const): 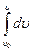= a ,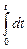

u - u ₀= аt.

Таким образом, при равнопеременном движении тела по прямой его скорость меняется со временем по закону:

u = u ₀± аt. (1.6)

Знак «плюс» в этой формуле соответствует равноускоренному движению, знак «минус» – равнозамедленному.

Теперь выведем зависимость координаты х тела от времени t при равноускоренном движении.

Выбрав ось координат 0Х вдоль направления движения тела, можно вновь записать: u =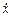, или

dx = udt = (u ₀ ± аt) dt.

Вновь полагая, что моменту времени t = 0соответствует координата х ₀, запишем:

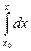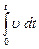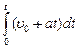= = = u ₀ t + ;

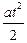х = х ₀+ u ₀ t + 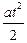. (1.7)

Какой знак («плюс» или «минус») следует поставить перед начальной скоростью u ₀ и ускорением а в уравнениях (1.6) – (1.7), зависит от того, совпадают ли (знак «плюс») или нет (знак «минус») направления соответственно векторов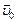и с направлением выбранной оси координат 0Х.

На рис. 1.4. приведены примеры графиков зависимостей от времени координаты, скорости и ускорения при равномерном, равноускоренном и равнозамедленном движении.

1.1.4 Движение вдоль прямой с переменным ускорением

Не нужно думать, что движение тела по прямой может быть только либо равномерным (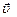 = const), либо равнопеременным ( = const). На практике часто возникают ситуации, когда ускорение тела (а, следовательно, и его скорость, как производная по времени от ускорения) меняются со временем. Простейший пример – гармонические колебания, в ходе которых координата тела меняется по синусоидальному (гармоническому) закону:

x = Asin (w t + a), (1.8)

u = 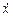= A w cos (w t + a) ¹ const,

a = 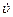==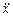 - A w² sin (w t + a) ¹ const.

Еще один пример движения, которое не является ни равномерным и ни равнопеременным – движение транспортного средства в режиме, когда меняется сила тяги F _ТЯГИ мотора. Как следует из второго закона Ньютона, для тела постоянной массы m ускорение a = F _ТЯГИ/ m, и, следовательно, изменение по какому-либо закону со временем силы тяги (например, вследствие использования водителем педали «газ») должно сопровождаться соответствующим изменением ускорения a тела.

В заключение заметим, что на практике часто используется понятие средней путевой скорости, которое применяется для характеристики движения с переменными скоростью и ускорением. В отличие от 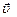эта скорость не является вектором и определяется, как отношение всего пройденного телом пути S ко всему затраченному времени D t, то есть u _СР = S/ D t.

1.1.5 Движение тела, брошенного под углом к горизонту

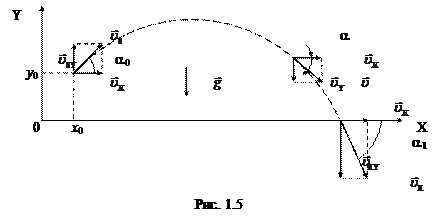
Если пренебречь действием силы сопротивления воздуха, траекторией такого движения этого тела окажется кривая – парабола. При этом такое движение можно представить в виде совокупности двух прямолинейных движений: одного (по горизонтали) – равномерного, его можно описать формулой (1.4), и, по вертикали, – равнопеременного, описываемого формулами (1.6 и 1.7).

Движение по горизонтали (ось 0X) является равномерным, так как в этом направлении на тело не действуют никакие силы, и, следовательно, ускорение тела в этом направлении равно нулю, то есть горизонтальная компонента вектора скорости u _X постоянна.

По вертикали на тело действует лишь одна постоянная сила – сила тяжести m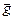, создающая постоянное же ускорение (примерно 9,8м/с). Следовательно, движение по вертикали является равнопеременным, и это означает, что компонента u _Y скорости тела вдоль вертикальной оси (обозначим её 0Y и направим в сторону, противоположную вектору 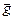) меняется по закону

u _Y = u _0Y- gt.

Соответственно, изменение координаты y описывается выражением y = y ₀ + u _0Y t - 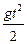. Учитывая связь компонент вектора скорости с самой скоростью (теорема Пифагора), а также с углом a, образуемым вектором 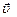с осью 0X (направленной вдоль поверхности Земли) – см. рис. 1.5, можно записать следующие пять формул, которые позволяют легко решать стандартные задачи кинематики для тела, траекторией которого является парабола:

х = х ₀ + u _X t

y = y ₀ + u _0Y t +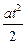

u _Y = u _0Y + аt

u =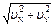

tg a = .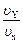

1.1.6 Движение точки по окружности

Для описания движения точки по окружности в декартовой системе координат необходимо знать законы изменения со временем хотя бы двух её линейных координат: x (t) и y (t) – см. рис. 1.6. Можно, однако, упростить задачу, перейдя от декартовых координат к полярным, в которых для описания движения по окружности достаточно знать радиус этой окружности r (который со временем не меняется), и всего лишь одну зависимость от времени – для угловой координаты (угла поворота j). В этом случае оказывается, что понятия, введённые для поступательного движения, не только могут быть использованы для описания движения по окружности, но и получаемые при этом формулы приобретают уже знакомый нам вид.

Итак, положение точки на плоскости мы будем задавать вектором 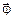, по величине, равным углу поворота относительно выбранной оси (на рисунке – это ось 0Y). Сам вектор 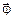(вектора такого типа называются аксиальными) направлен вдоль оси вращения в соответствии с «правилом винта (буравчика)»: поворачивая винт в сторону возрастания угла, определяем, куда движется тело самого винта – это и есть направление вектора 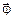. На рис. 1.6, на котором увеличению угла соответствует вращательное движение точки A по часовой стрелке, вектор 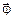направлен из точки 0 по оси вращения вглубь плоскости рисунка.

По определению вектор

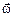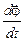= (1.9)

называется угловой скоростью движения точки по окружности. В СИ величину угла принято измерять в радианах, единица измерения угловой скорости – рад × с ^-1. Вектор 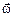также направлен вдоль оси вращения: в ту же сторону, что и 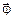, если при вращении угол растёт, или в противоположную, если угол j уменьшается. На рис. 1.6 вектор 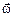так же, как и 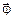, направлен вдоль оси вращения «от нас».

Угловым ускорением 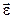называется скорость изменения угловой скорости:

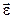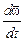= , (1.10)

величина углового ускорения измеряется в рад × с ^-2. Если в процессе движения угловая скорость растёт, значит, вектор 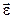направлен в ту же сторону, что и вектор 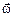, если угловая скорость уменьшается, то вектор 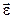хотя и направлен вдоль оси вращения, но антипараллелен вектору .

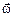Равномерным называется вращение, при котором 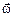= const. Действуя так же, как в случае рассмотрения равномерного движения точки по прямой, можно легко показать, что при таком движении зависимость угла поворота от времени будет выражаться формулой

j = j₀ + w t (1.11)

Здесь j₀ – значение угла в начальный (t = 0) момент времени; знак перед вторым слагаемым зависит от того, в какую сторону направлен вектор 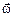: если при движении точки угол j растёт, то тогда пишем «+», если уменьшается (становится меньше j₀) – знак «-».

Время T, за которое совершается один полный оборот (при этом j - j₀ = 2p), называется периодом обращения точки вокруг оси. Таким образом,

w = 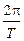. (1.12)

Равнопеременным называется движение по окружности, при котором 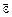= const. При этом если 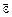↑↑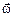, вращение называется равноускоренным, а если 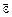↑↓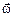– равнозамедленным.

Аналогично тому, как это было сделано при выводе формул (1.6) и (1.7), можно показать, что при равнопеременном вращении с начальной скоростью w₀ зависимости w(t) и j(t) имеют вид:

w = w₀± e t; (1.13)

j=j₀+w₀ t ± 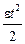. (1.14)

Перед значениями w₀ и e для тех из векторов 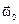и 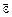, которые направлены в сторону, противоположную вектору 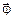, в формулах (1.13) и (1.14) пишется знак «минус».

В каждый момент времени величина линейной скорости точки u при движении по окружности радиусом r связана с её угловой скоростью соотношением u = w r. Если точка движется по траектории сложной формы, то в каждый момент времени для положения, характеризующегося радиус-вектором 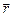, проведённым из любой заданной точки, её линейную и угловую скорости относительно этой точки можно связать формулой

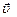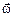
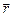= []. (1.15)

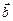Произведение и вида 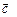= [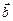] называется векторным; его результатом является вектор 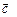такой, что c = ab × sin a (здесь a – угол между векторамии 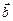). Направление вектора 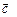определяется по правилу буравчика или по «правилу левой руки»: пальцы ладони направляются по вектору так, чтобы вектор 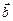«входил» в ладонь, при этом отставленный в сторону большой палец будет показывать направление .

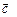При движении по окружности все три вектора (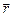, 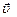и 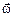) оказываются взаимно перпендикулярными, то есть, формула (1.15) приобретает вид u = w r. Используя «правило левой руки» для рис. 1.6, то есть, направляя пальцы ладони по радиус-вектору 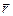так, чтобы вектор линейной скорости точки 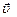«входил» в ладонь, по отставленному в сторону большому пальцу находим направление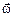(из точки 0 по оси вращения вглубь плоскости рисунка).

Равнопеременное движение по любой кривой означает, что вектор линейной скорости 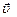непрерывно меняет свою величину. Соответствующее этому явлению линейное ускорение 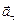называется тангенциальным, в общем случае оно связано с угловым ускорением 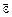векторным произведением

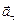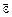
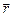= []. (1.16)

В частности, при равнопеременном движении по окружности a_t = e r, поскольку вектора 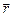, 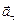и 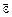взаимно перпендикулярны.

Если e = 0, то w = const, и движение по окружности является равномерным. Но даже в этом случае вектор скорость 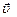меняется – по направлению. Это означает, что имеет место ускорение 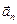, которое называется нормальным (или центростремительным 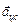) и при этом направлено перпендикулярно вектору 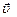в сторону центра окружности, по которой движется точка. Можно показать, что

a_цс = 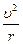, или, с учётом формулы (1.15), a_цс = w² r. (1.17)

Движение по прямой можно представить, как движение по окружности бесконечно большого радиуса, при этом 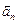= 0, а 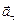совпадает с обычным линейным ускорением точки . При равномерном движении по окружности нулю равно тангенциальное ускорение 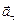, то есть = 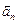. В общем случае при движении с ускорением по любой кривой полное ускорение точки является векторной суммо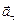й и 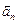, а поскольку они взаимно перпендикулярны, то

a = 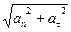. (1.18)

Сказанное поясняется рисунком 1.7.

Таким образом, в рамках данной лекции, мы показали как, основываясь лишь на определениях и используя при этом известные математические операции, можно построить основы целого раздела физики, описывающего перемещение тела в пространстве и позволяющего, тем самым, решать важные в практическом отношении задачи.

Некоторые примеры

О пути

- Длина первой железной дороги России, построенной в 1837 году, (Петербург – Царское село) – 26 км.

- Длина железнодорожной магистрали Москва – Санкт-Петербург (открыта в 1851 году) – 650 км.

- Длина самого длинного в мире железнодорожного тоннеля (Симплтон I, Швейцария) – 19,825 км.

- Длина Северо-Муйского тоннеля (Байкало-Амурская магистраль) – около 15 км;

- Длина самой большой в мире электрифицированной магистрали (Брест – Минск – Москва – Омск – Иркутск – Хабаровск – Уссурийск) – 10400 км.

- Тормозной путь электрички – до 0,5 км.

- Тормозной путь поезда (зависит от массы и скорости состава) – до 2 км.

О скорости

При описании движения тел термин «скорость» может использоваться в более широком, чем это соответствует формуле (1.1) смысле. Так, можно говорить о крейсерской скорости транспортного средства (эта скорость соответствует движению по маршруту без учёта участков разгона и торможения), о коммерческой скорости (эта скорость характеризует движение груза по маршруту с учётом всех задержек, связанных с перегрузкой с одного транспортного средства на другое, с оформлением документации и т. д.), о конструкционной скорости (максимальной скорости, закладываемой конструктором в проектируемый объект), и др. Каждый такой «вид» скорости имеет собственное определение, поскольку позволяет ответить на вполне определённые практически значимые вопросы. В частности, как мы уже говорили выше, на практике помимо введённой нами мгновенной скорости 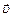используется понятие средней путевой скорости.

В СИ время измеряется в секундах, поэтому единицей измерения скорости является метр в секунду: [ u ] = м×с^-1. Допускается использование и других единиц измерения: км/ч, км/c, см/cи др.

- Максимальная скорость первого паровоза (1803 г., Р. Третвитик, Англия) – 10 км/ч.

- Скорость паровоза «Ракета» (1829 г., Д. Стефенсон, Англия) – 50 км/ч.

- Скорость первого российского паровоза (1834 г., отец и сын Черепановы) – 15 км/ч.

- Скорость поезда на трассе Париж – Бордо, Франция – до 350 км/ч.

- Рекорд скорости для обычных поездов на скоростной трассе Париж – Страсбург – до 574,8 км/ч (2007 г.).

- Скорость экспериментальной модели поезда, движущегося в специально проложенной вакуумной трубе (Япония) – до 2535 км/ч.

- Скорость звука в воздухе – 330 м/с = 1188 км/ч.

- Скорость света в вакууме – 2,98×10⁸ м/с

Об ускорении

Единица измерения ускорения в СИ: [ а ] = м×с^-2.

Некоторые примеры.

- Обычное ускорение при начале движения поезда – до 0,3 м/с².

- Допустимое ускорение поезда (считается при больших ускорениях у пассажиров возникают ощутимые неудобства) – 1,5 м/с²;

- Ускорение поезда при экстренном торможении – около 1 м/с²

- Ускорение, возникающее при использовании специально разрабатываемых тормозов для скоростных поездов – до 1,9 м/с².

Вопросы для повторения

1. Дайте определения основных терминов, используемых в кинематике: траектории, пути, перемещения, скорости, ускорения, средней скорости.

2. Какие виды движения точки по прямой и по окружности Вам известны? Дайте определения этим видам движения.

3. Выведите формулы, описывающие изменение со временем координаты точки при её движении по прямой в случаях разных видов движения.

4. Запишите формулы, описывающие изменение со временем координат точки при её движении по параболе.

5. Выведите формулы, описывающие изменение со временем угловой координаты точки при её движении по окружности в случаях разных видов движения.

6. Дайте определения основных параметров, используемых при описании движения точки по окружности.

7. Как связаны между собою линейные и угловые характеристики движения тела по окружности?

8. Приведите примеры характерных значений расстояний, скоростей и ускорений, с которыми мы сталкиваемся на железнодорожном транспорте.

Каково максимально достижимое значение скорости в нашей Вселенной? Какой физический объект имеет эту скорость?

Дата добавления: 2013-12-11