Всякое действие носит характер взаимодействия; силы взаимодействия равны по величине и противоположны по направлению

Первый закон Ньютона: существуют такие системы отсчёта, в которых тело движется равномерно прямолинейно или покоится до тех пор, пока внешние воздействия не выведут его из этого состояния.

Таким образом: а) вслед за Ньютоном мы постулируем наличие таких систем отсчёта, в которых выполняется закон, и б) мы делаем вывод о том, что в данной системе отсчёта тело будет двигаться равномерно прямолинейно или покоиться, если на него не действуют внешние силы.

В реальности, конечно, невозможно представить себе тело, на которое вообще никакие силы не действуют: на все объекты, например, действуют силы гравитационного притяжения со стороны других тел. Но поскольку сила является вектором, может оказаться, что сумма всех сил, действующих на тело со стороны других объектов, равна нулю (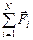= 0), и тогда, действительно, скорость тела будет постоянной (или даже равной нулю).

Системы отсчёта, в которых выполняется этот закон, называются инерциальными.

Таким образом, инерциальными являются любые системы отсчёта, которые покоятся друг относительно друга, или одна из них движется относительно другой равномерно прямолинейно.

Следует помнить, что равномерное прямолинейное движение в природе встречается достаточно редко и длится недолго. Так, например, с домом у дороги и с проезжающим мимо него с заданной скоростью автомобилем можно связать инерциальные системы отсчёта, однако следует помнить, что поверхность Земли не является плоскостью, а, значит, организовать по её поверхности прямолинейное движение не так-то легко.

Сама Земля вращается как вокруг своей оси, так и вокруг Солнца, поэтому системы отсчёта, связанные с Солнцем и Землёй, вообще говоря, инерциальными считать тоже нельзя…

2.2.2 Второй закон Ньютона

Как правило, любое тело одновременно испытывает воздействие со стороны многих объектов, то есть на него действует не одна, а несколько сил. Согласно второму закону Ньютона сумма всех сил, действующих на тело, равна скорости изменения его импульса:

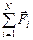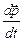= . (2.2)

Заметим, что сила – вектор, и суммирование в этой формуле должно производиться по правилам сложения векторов (по правилу параллелограмма или же по отдельности для каждой из проекций сил).

Формулировка закона ещё раз напоминает нам, что скоростью изменения какой-либо функции (в нашем случае – импульса) называется первая производная этой функции по времени.

Проанализируем выражение (2.2).

Сумму всех сил, действующих на тело, заменим одной результирующей силой:

= .

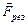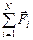Воспользовавшись определением импульса, распишем, чему равна скорость его изменения:

.

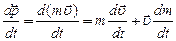По определению ускорения – см. формулу (1.2):

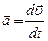, то есть .

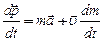Если масса тела не меняется в процессе его движения (m = const, или 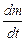= 0), то формула (2.2) приобретает вид, хорошо известный из школьного курса физики:

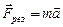. (2.3)

Таким образом, известное выражение (2.3) справедливо лишь для случая, когда масса тела, движущегося под действием некоторой постоянной силы 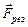, не меняется со временем.

Давайте ответим на вопрос, меняется ли в процессе движения

- масса грузовика? (Да? Нет?)

- масса самолёта? (Да? Нет?)

- масса стартующей ракеты? (Да? Нет?)

В последнем случае очевиден ответ – «Да», поскольку при взлете ракеты сжигаются десятки тонн горючего (да и ставшие пустыми баки разгонных ступеней сбрасываются). Но горючее сжигается и при полёте самолёта, и при движении грузовика! Просто соответствующим изменением массы мы зачастую пренебрегаем по сравнению с массой самого движущегося объекта: именно поэтому при решении школьных задач из раздела «динамика» мы привыкли использовать формулу второго закона Ньютона не в виде (2.2), а в виде (2.3).

Существует ещё одно важное соображение, которое необходимо иметь в виду, когда мы говорим, что именно формула (2.2), а не (2.3) является основной для второго закона.

Дело в том, что импульс тела с увеличением его скорости возрастает не прямо пропорционально u. Более общая по сравнению с классической механикой теория – специальная теория относительности – говорит о том, что на самом деле импульс тела связан с его скоростью соотношением

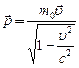, (2.4)

где m ₀ – масса покоящегося тела (масса покоя); с – скорость света в вакууме.

Дробь 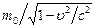в формуле (3.5) часто интерпретируется, как масса m тела, движущегося со скоростью u:

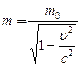, (2.5)

Сказанное означает, что по мере разгона тела его масса увеличивается. Особенно заметным это оказывается при достижении скоростей, близких к скорости света: при u << с (что как раз и имеет место в классической механике) подкоренное выражение в формулах (2.4) и (2.5) практически равно единице, и m» m ₀. Однако, если всё же учесть возможность разгона тела до больших скоростей, то понятно, что формула второго закона Ньютона в виде (2.3) при этом перестанет работать, в то время как выражение (2.2) с учётом формулы (2.4) для импульса будет по-прежнему оставаться справедливым.

Для современных науки и техники процессы, в которых подтверждается справедливость релятивистских (от английского relatiuity – относительность) соотношений (2.4) и (2.5), стали уже вполне обыденными, не вызывает сомнений и корректность приведённой выше формулировки второго закона Ньютона. Тем удивительнее то, что Ньютон, живший за две с лишним сотни лет до создания СТО, сформулировал свой второй закон именно в виде (2.2) – общем, справедливом даже в релятивистской физике, а не в упрощённом (2.3), который применим только в физике классической (и то лишь, если m = const).

В заключение заметим, что формулы (2.2) и (2.3) позволяют определить единицу измерения силы. В СИ сила измеряется в ньютонах; 1 Н =1 кг×м / с ².

2.2.3 Третий закон Ньютона. Вес тела

Пример: Тело, подвешенное на нити, на пружине, лежащее на твёрдой поверхности, плавающее в жидкости действует на свою опору (нить, пружину, твёрдую поверхность, жидкость) с некоторой силой .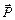

Сила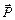, с которой тело действует на опору, называется весом тела.

Вес и сила реакции опоры приложены к разным телам и поэтому не могут уравновешивать друг друга!

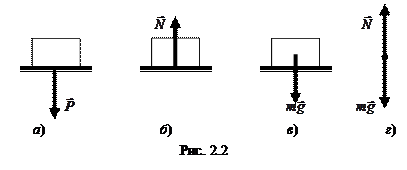
На рис. 2.2. а) изображен кубик, лежащий на полу. Вес – это сила 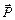, приложенная к поверхности пола; под действием этой силы пол немного прогибается. В свою очередь, пол действует на нижнюю часть тела с силой (сила реакции опоры) – рис. 2.2. б). Кроме силы на тело действует сила тяжести , приложенная к центру кубика – рис. 2.2. в). Поскольку кубик не вращается, его можно считать материальной точкой, к которой приложены всего две силы: и – рис. 2.2. г), причём в состоянии покоя должно выполняться условие:

+ = 0. (2.6)

Так как по третьему закону Ньютона

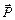= - , (2.7)

то это означает, что в состоянии покоя

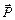= , (2.8)

Если же кубик движется с ускорением (лежит на полу движущейся с ускорением кабины лифта), согласно второму закону Ньютона для него следует записать:

+ = m , (2.9)

что, с учётом формулы (2.8), означает:

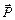= - m . (2.10)

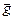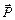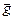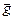Если вектор направлен туда же, куда и вектор , вес тела будет меньше силы тяжести (при = вес вообще исчезнет, наступит состояние невесомости). Если же вектора и направлены в противоположные стороны, возникает состояние перегрузки: вес тела оказывается больше его силы тяжести.

2.2.4 Закон Всемирного тяготения

Как мы уже говорили, в природе существуют четыре вида фундаментальных взаимодействий, одним из которых является гравитационное. В основе классической теории гравитации лежит открытый Ньютоном закон Всемирного тяготения, согласно которому:

– все тела в природе притягиваются друг к другу;

– сила притяжения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;

– если тела – однородные шары, сферы или их можно считать точечными, справедлива формула (см. рис. 2.3)

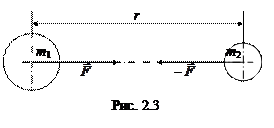F = G 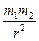. (2.11)

В этой формуле G = 6,67×10^-11м³×кг^-1с^-2 – гравитационная постоянная, m ₁ – масса первого тела, m ₂ – масса второго тела, r – расстояние между центрами тел (шаров, сфер), F – сила их гравитационного притяжения.

С некоторыми примерами применения этого закона мы встретимся позднее.

2.2.5 Примеры сил. Рекомендации к решению стандартных

задач по физике

· Если в задаче встречается слово «сила», следует вспомнить формулу второго закона Ньютона. При этом если масса тела, о котором идёт речь в задаче, постоянна, то:

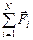= m . (2.12)

Далее необходимо:

– на чертеже изобразить все силы, действующие на тело, о котором идёт речь в задаче;

– начертить оси координат (одну из осей удобно направлять вдоль направления вектора ускорения тела );

– изобразить проекции всех сил на выбранные оси;

– формулу (2.12) переписать для проекций сил.

· Если в задаче идёт речь о весе тела, для её решения следует переходить от веса к силе реакции опоры:

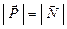. (2.13)

Это связано с тем, что к телу приложена именно сила реакции опоры, а не вес, то есть в формуле (2.12) должна фигурировать сила , а не .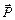

· Если в задаче идёт речь о коэффициенте трения скольжения, для её решения следует записать формулу

F _ТР = m N, (2.14)

где F _ТР – сила трения скольжения, N – сила реакции опоры, m – коэффициент трения скольжения (зависит, прежде всего, от природы трущихся тел).

· Если в задаче идёт речь о пружине, для её решения следует записать формулу:

F _УПР = - kx, (2.15)

где F _УПР – сила упругости, с которой пружина действует на объект; x – смещение объекта от положения равновесия, k – коэффициент жёсткости пружины, который зависит от свойств материала, из которого изготовлена пружина, от её размеров и формы[2].

При решении задач полезно помнить, что коэффициент жёсткости k входит также в выражение для потенциальной энергии упруго деформированной пружины W _П = ½ kx ², которое мы выведем на одной из следующих лекций, а также в формулу для периода гармонических колебаний тела на пружине (пружинного маятника) T = 2p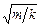(её мы выведем в начале следующего семестра).

· Если в задаче идёт речь о спутниках, планетах, других космических объектах, для её решения необходимо записать формулу (2.11) закона Всемирного тяготения.

· Если в задаче идёт речь о теле, погружённом в жидкость (газ), для её решения следует записать формулу закона Архимеда:

F _ВЫТ = r_Ж gV _ТЕЛА. (2.16)

Здесь F _ВЫТ – выталкивающая сила, r_Ж – плотность жидкости (газа), V _ТЕЛА – объём части тела, погружённой в жидкость (газ).

· Если в задаче идёт речь о взаимодействующих точечных зарядах, следует записать формулу закона Кулона. Согласно этому закону:

– разноимённо заряженные тела притягиваются друг к другу, одноимённо заряженные – отталкиваются;

– сила взаимодействия тел прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними;

– если тела – однородно заряженные шары, сферы или их можно считать точечными зарядами, справедлива формула (см. рис. 2.4)

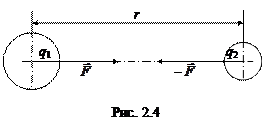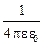
F = 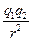. (2.17)

В формуле (2.17) e₀ = 8,85×10^-12Ф/м– электрическая постоянная, q ₁ – заряд первого тела, q ₂ – заряд второго тела (на рис. 2.4 знаки зарядов противоположные), r – расстояние между центрами тел (шаров, сфер), e – диэлектрическая проницаемость среды, в которой находятся тела, F – сила их электростатического взаимодействия.

Как мы отметим далее, если хотя бы одно из взаимодействующих заряженных тел – не точечное, не равномерно заряженные шарик или сфера, напрямую формулой закона Кулона пользоваться нельзя, следует выразить силу 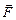, действующую на заряд q через напряженность электрического поля 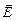, в котором находится заряд:

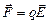. (2.18)

Типичная ситуация, описываемая этой формулой – поведение точечного заряда, шарика, покоящегося или движущегося в однородном электрическом поле.

· Если в задаче идёт речь о проводнике с током, находящемся в магнитном поле, следует записать формулу для силы Ампера:

F _А = BIlsin a. (2.19)

Здесь B – индукция магнитного поля, в котором находится прямой проводник длиной l, по которому идёт ток I, a – угол между направлением протекания тока и направлением вектора 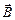. Направление вектора силы 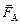, действующей на проводник с током, находится по правилу левой руки.

· Если в задаче идёт речь об электрическом заряде, движущемся в магнитном поле, для её решения следует записать формулу силы Лоренца:

F _Л = Bqusin a. (2.20)

В этой формуле B – индукция магнитного поля, q – заряд, движущийся со скоростью u, a – угол между направлением скорости заряда и направлением вектора 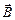. Направление вектора силы 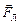, действующей на движущийся положительный заряд, находится по правилу левой руки. Если заряд – отрицательный, то найденное по правилу левой руки направление силы следует поменять на противоположное.

· Если в задаче идёт речь о теле, находящемся в состоянии покоя (или равномерного прямолинейного движения), следует записать:

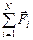= 0. (2.21)

Некоторые примеры

О массе

- Электрон – 9,1×10^-31 кг.

- Пуля автомата Калашникова – 7,4×10^-3 кг.

- Первый искусственный спутник Земли – 83,6 кг.

- Автомобиль «Волга» (ГАЗ-24) – 1,42×10³ кг.

- Слон – до 4,5×10³ кг.

- Трактор К-700 – 11×10³ кг.

- Четырёхосный железнодорожный грузовой вагон – 22,6×10³ кг.

- Цельнометаллический пассажирский вагон – 54×10³ кг.

- Самый большой из добытых китов – 150×10³ кг

- Электровоз ВЛ10 – 184×10³ кг.

- Обычная масса грузового поезда – до 24000×10³ кг.

- Масса самых тяжелых поездов, проведенных в порядке эксперимента, превышает 40000×10³ кг.

- Останкинская телевизионная башня – 55000×10³ кг.

О силе тяги

- Первый паровоз «Ракета» Стефенсона – до 2,8 кН.

- Трактор колёсный К-700 при скорости 2,6 км/ч – 60 кН.

- Двухсекционный тепловоз 2ТЭ10 при скорости 24 км/ч – 510 кН.

- Тепловоз ТЭ3 при скорости 20 км/ч – 400 кН, при трогании с места – 610 кН.

- Электровоз ВЛ80^к при скорости 51,6 км/ч – 460 кН.

- Электровоз ВЛ10 при скорости 47,3 км/ч – 390 кН.

- Суммарная тяга двигателей первой ступени ракеты-носителя корабля «Восток» – 5000 кН.

- Суммарная тяга двигателей ракеты-носителя «Энергия» в начале полёта – 353000 кН.

Вопросы для повторения

1. Что называется импульсом материальной точки? Импульсом системы материальных точек?

2. Что называется системой отсчёта? Что такое инерциальная система отсчёта? Приведите примеры.

3. Сформулируйте первый закон Ньютона, приведите примеры его проявления.

4. Сформулируйте второй закон Ньютона, приведите примеры его проявления.

5. Продемонстрируйте, в каком случае из формулы второго закона Ньютона, записанной в общем виде, можно получить упрощённое соотношение F = ma.

6. Сформулируйте третий закон Ньютона, приведите примеры его проявления.

7. Какие действия следует предпринять при решении задачи, если в ней встречается понятие «силы»?

8. Перечислите основные виды сил, встречающихся при решении стандартных задач по физике, и запишите соответствующие формулы.

Сформулируйте закон Всемирного тяготения. Ответ поясните рисунком.

Дата добавления: 2013-12-11