Лекция 1. Функции нескольких переменных

Функции нескольких переменных. Геометрическое изображение функции двух переменных. Линии и поверхности уровня. Предел и непрерывность функции нескольких переменных, их свойства. Частные производные, их свойства и геометрический смысл.

Определение 1.1. Переменная z (с областью изменения Z)называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.

Обозначения: z = f(x,y), z = z(x,y).

Примеры.

1. z = xy, z = x ² + y ² - функции, определенные для любых действительных значений х,у.
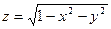2. - функция, областью определения которой являются решения неравенства .

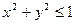Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 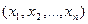, являющихся аргументами функции нескольких переменных.

Определение 1.3.. Переменная z (с областью изменения Z)называется функцией нескольких независимых переменных 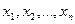в множестве М, если каждому набору чисел 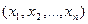из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.

Обозначения: z = f 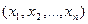, z = z .

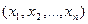Геометрическое изображение функции двух переменных.

Рассмотрим функцию z = f(x,y), (1.1)

определенную в некоторой области М на плоскости О ху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где 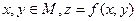, является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.

z

z = f(x,y)

M y

Примерами могут служить изучаемые в предыдущем семестре уравнения плоскости

z = ax + by + c

и поверхностей второго порядка:

z = x ² + y ² (параболоид вращения),

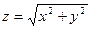(конус) и т.д.

Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n -мерном пространстве», хотя изобразить подобную поверхность невозможно.

Линии и поверхности уровня.

Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости О ху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.

Пример.

Найдем линии уровня для поверхности z = 4 – x ² - y ². Их уравнения имеют вид x ² + y ² = 4 – c (c =const) – уравнения концентрических окружностей с центром в начале координат и с радиусами 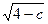. Например, при с =0 получаем окружность x ² + y ² = 4.

Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.

Пример.

Для функции u = 3 x + 5 y – 7 z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3 x + 5 y – 7 z –12 + с = 0.

Дата добавления: 2013-12-12