Дифференцирование сложных функций

Пусть аргументы функции z = f (x, y) являются, в свою очередь, функциями переменных u и v: x = x (u, v), y = y (u, v). Тогда функция f тоже есть функция от u и v. Выясним, как найти ее частные производные по аргументам u и v, не делая непосредственной подстановки

z = f (x(u, v), y(u, v)). При этом будем предполагать, что все рассматриваемые функции имеют частные производные по всем своим аргументам.

Зададим аргументу u приращение Δ u, не изменяя аргумент v. Тогда

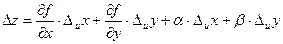. (2.7)

Если же задать приращение только аргументу v, получим: 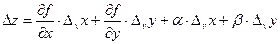. (2.8)

Разделим обе части равенства (2.7) на Δ u, а равенства (2.8) – на Δ v и перейдем к пределу соответственно при Δ u→ 0 и Δ v→ 0. Учтем при этом, что в силу непрерывности функций х и у 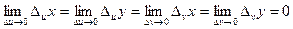. Следовательно,

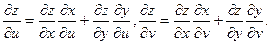(2.9)

Рассмотрим некоторые частные случаи.

Пусть x = x(t), y = y(t). Тогда функция f (x,y) является фактически функцией одной переменной t, и можно, используя формулы (2.9) и заменяя в них частные производные х и у по u и v на обычные производные по t (разумеется, при условии дифференцируемости функций x(t) и y(t)), получить выражение для :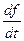

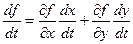(2.10)

Предположим теперь, что в качестве t выступает переменная х, то есть х и у связаны соотношением у = у (х). При этом, как и в предыдущем случае, функция f является функцией одной переменной х. Используя формулу (2.10) при t = x и учитывая, что 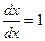, получим, что 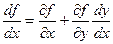. (2.11)

Обратим внимание на то, что в этой формуле присутствуют две производные функции f по аргументу х: слева стоит так называемая полная производная, в отличие от частной, стоящей справа.

Примеры.

1. Пусть z = xy, где x = u ² + v, y = uv ². Найдем 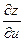и 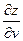. Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов:

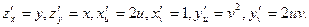Тогда из формулы (2.9) получим: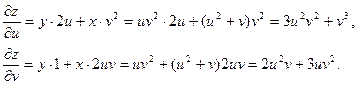

(В окончательный результат подставляем выражения для х и у как функций u и v).

2. Найдем полную производную функции z = sin (x + y ²), где y = cos x.

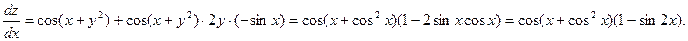
Дата добавления: 2013-12-12