Формула Тейлора для функции нескольких переменных

Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала. Формула Тейлора для функции нескольких переменных. Производная функции по направлению. Градиент и его свойства.

Пусть функция z = f (x, y) является дифференцируемой в окрестности точки М (х₀, у₀). Тогда ее частные производные 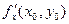и 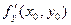являются угловыми коэффициентами касательных к линиям пересечения поверхности z = f (x, y) с плоскостями у = у₀ и х = х₀, которые будут касательными и к самой поверхности z = f (x, y). Составим уравнение плоскости, проходящей через эти прямые. Направляющие векторы касательных имеют вид {1; 0; 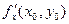} и {0; 1; 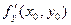}, поэтому нормаль к плоскости можно представить в виде их векторного произведения: n = {-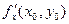,-,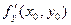 1}. Следовательно, уравнение плоскости можно записать так:

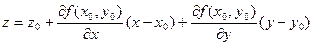, (4.1)

где z₀ = .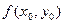

Определение 4.1. Плоскость, определяемая уравнением (4.1), называется касательной плоскостью к графику функции z = f (x, y) в точке с координатами (х₀, у₀, z₀).

Из формулы (2.3) для случая двух переменных следует, что приращение функции f в окрестности точки М можно представить в виде:

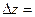
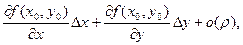или

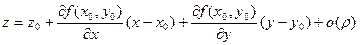(4.2)

Следовательно, разность между аппликатами графика функции и касательной плоскости является бесконечно малой более высокого порядка, чем ρ, при ρ→ 0.

При этом дифференциал функции f имеет вид:

,

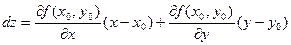что соответствует приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.

Определение 4.2. Ненулевой вектор, перпендикулярный касательной плоскости в точке М (х₀, у₀) поверхности z = f (x, y), называется нормалью к поверхности в этой точке.

В качестве нормали к рассматриваемой поверхности удобно принять вектор -- n = {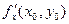,,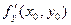-1}.

z

z = f (x,y)

M₀ (x₀, y₀, z₀)

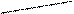n

y

M (x₀, y₀)

x

Пример.

Составим уравнение касательной плоскости к поверхности z = xy в точке М (1; 1). При х₀ = у₀ = 1 z₀ = 1; 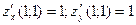. Следовательно, касательная плоскость задается уравнением: z = 1 + (x – 1) + (y – 1), или x + y – z – 1 = 0. При этом вектор нормали в данной точке поверхности имеет вид: n = {1; 1; -1}.

Найдем приращение аппликат графика функции и касательной плоскости при переходе от точки М к точке N (1,01; 1,01).

Δ z = 1,01² - 1 = 0,0201; Δ z _кас = (1,01 + 1,01 – 1) – (1 + 1 – 1) = 0,02. Следовательно,

dz = Δ z _кас = 0,02. При этом Δ z – dz = 0,0001.

Как известно, функцию F(t) при условии существования ее производных по порядок n +1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа (см. формулы (21.7), (21.11) первой части курса). Запишем эту формулу в дифференциальной форме:

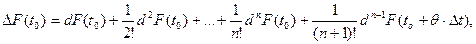(4.3)

где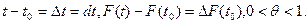

В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.

Рассмотрим функцию двух переменных f(x, y), имеющую в окрестности точки (х₀, у₀) непрерывные производные по (n + 1)-й порядок включительно. Зададим аргументам х и у некоторые приращения Δ х и Δ у и рассмотрим новую независимую переменную t:

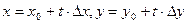(0 ≤ t ≤ 1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х₀ , у₀) и (х₀ + Δ х, у₀ + Δ у). Тогда вместо приращения Δ f (x₀,y₀) можно рассматривать приращение вспомогательной функции

F(t) = f (x₀ + t Δ x, y₀ + t Δ y), (4.4)

равное Δ F (0) = F ( 1) – F (0). Но F (t) является функцией одной переменной t, следовательно, к ней применима формула (4.3). Получаем:

.

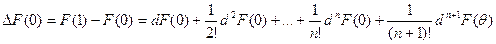Отметим, что при линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть

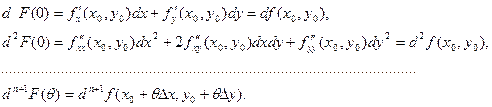
Подставив эти выражения в (4.3), получим формулу Тейлора для функции двух переменных:

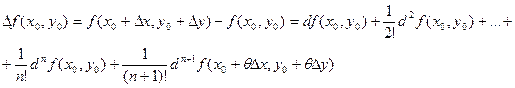, (4.5)

где 0<θ<1.

Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

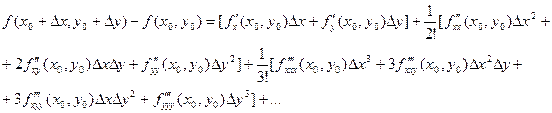
Дата добавления: 2013-12-12