Основные правила дифференцирования

Схема вычисления производной

Дифференцируемость функции

Нахождение производной функции называется ее дифференцированием.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке.

Теорема о зависимости между непрерывностью и днфференцируемостью функции: если функция дифференцируема в точке, то она в этой точке непрерывна.

Без доказательства.

Замечание: обратное утверждение в общем случае не является верным, т.е. если функция непрерывна в данной точке, то она не обязательно в ней дифференцируема. Непрерывность функции является необходимым, но не достаточным условием ее дифференцируемости.

Приведем пример функции, которая, являясь непрерывной в точке
х = 0, при этом недифференцируема в этой точке. На рисунке 3.2 представлен график функции у = |х|. Она непрерывна в точке
х = 0. Производная функция (если она существует) равна 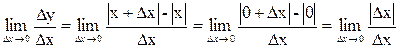. Последний предел не существует, так как односторонние пределы в этой точке не совпадают (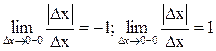). Следовательно, производная в точке х = 0 не существует (геометрически это означает отсутствие касательной к кривой в точке х = 0).

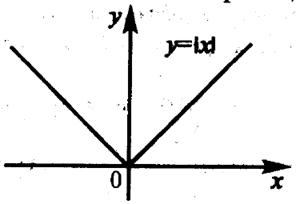
Схема нахождения производной функции у = f(х) включает следующие этапы:

1. Дают аргументу х приращение Dх ¹ 0 и находят значение функции
у = f(х + Dх).

2. Находят приращение функции Dу = f(х + Dх) - f(х).

3. Составляют отношение Dу/Dх.

4. Находят его предел при Dх ® 0 (если этот предел существует).

Рассмотрим эти этапы на примере функции у = х³. Чтобы найти ее производную, дадим аргументу приращение Dх ¹ 0 и найдем у = f(х + Dх) =
= (х + Dх)³ = х³ + 3х²Dх + 3хDх² + Dх³. Затем найдем приращение функции
Dу = f(х + Dх) - f(х) = f(х + Dх) - х³ = 3х²Dх + 3хDх² + Dх³ = Dх (3х² + 3хDх +
+ Dх²). Составим отношение Dу/Dх = 3х² + 3хDх + Dх². Найдем его предел .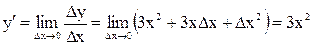

Можно доказать, что для любого n (xⁿ)` = nx^n-1.

Рассмотрим их без доказательства.

1. Производная постоянной равна нулю, т.е. с' = 0 (это очевидно, так как любое приращение постоянной функции равно нулю).

2. Производная аргумента равна 1, т.е. х` = 1 (правило следует из формулы для производной степенной функции).

3. Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
(u + v)' = u' + v'.

4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (uv)'=u'v + v'u.

Следствие 1. Постоянный множитель можно выносить за знак производной: (сu)' = сu'.

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: (uvw)' = u'vw + uv'w + + uvw'.

5. Производная частного двух дифференцируемых функций может быть найдена по формуле .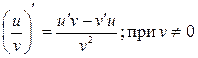

6. Если у = f(u) и u = j(х) - дифференцируемые функции от своих аргументов, то производная сложной функции у = f([j(х)]) существует и равна производной данной функции по промежуточному аргументу u, умноженной на производную самого промежуточного аргумента по независимой переменной х: y` = f `(u)*u`.

7. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции: .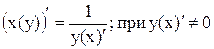

Проиллюстрируем последнее правило на примере взаимно обратных функций, производные которых мы уже знаем. Возьмем степенную функцию y = x³, y` = 3x². Такую же производную можно получить, если воспользоваться обратной функцией. В самом деле, 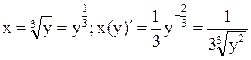. По правилу .

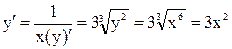Дата добавления: 2013-12-12