Свойства собственных значений и собственных чисел

Матричная запись линейных операторов.

Понятие линейного оператора. Основные свойства. Собственные числа и собственные векторы. Квадратичные формы.

Лекция 16.

Цель: Изучить понятия линейного оператора и его собственных чисел и собственных векторов, методы их нахождения.

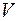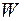Определение. Пусть и – линейные пространства размерност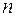и и 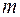соответственно, – будем называть оператором, действующим из 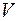и

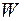
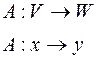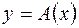, или 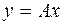, говорят что y – образ элемента x, а x – прообраз y.

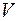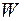Определение. Оператор , действующий из в называется линейным, если для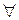 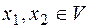и 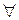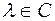выполняются соотношения:

1. .

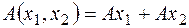2. .

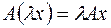Если 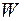(комплексная плоскость), то – называют линейным функционалом. Если 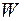совпадает с 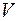, то – называют линейным преобразованием пространства.

Определение. Произведение λ на называется оператор λA определяемый равенством 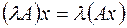. 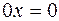, где 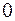нулевой оператор,

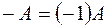, противоположный оператор. 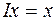- I – т ождественный или единичный оператор.

Определение. Произведением оператора на 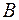называется оператор, для которого верны следующие соотношения :

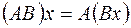1);

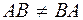2);

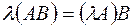3);

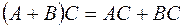4);

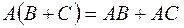5).

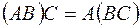Определение. Оператор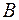называется обратным для если, 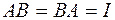, обозначают .

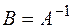Определение. Ядром линейного оператора называется множество всех элементов 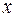пространства 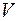, для которых : .

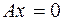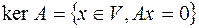Определение. Образом линейного оператора называется множество элементов 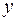таких что : .

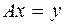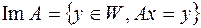Определение. Рангом линейного оператора называется число равное .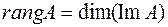

Теорема. Пусть 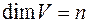и пусть 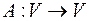, тогда .

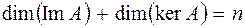Фиксируем в линейном пространстве 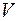базис 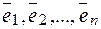пусть 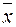– произвольный элемент 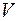и 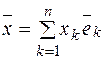(разложение 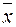по базису ).

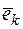Пусть – линейный оператор 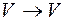. Тогда имеем ,

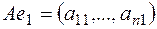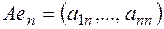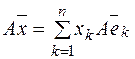…,. . Пусть 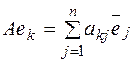образы базисных векторов, тогда 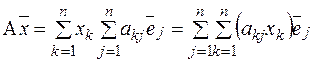, т. е. 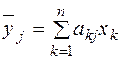, j=1,…,n, .

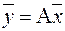Рассмотрим 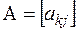матрицу линейного оператора в заданном базисе 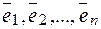, это матрица столбцами которой являются координаты базисных векторов 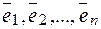. Причем единственный линейный оператор , матрицей которого в заданном базисе 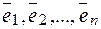будет матрица .

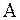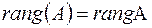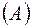, - оператор.

При этом соотношения 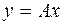, , 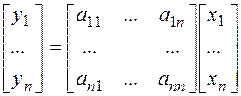с одной стороны связывают образ 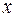с координатами прообраза 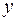, с другой стороны, описывают действие линейного оператора заданного матрицей A. При изменении базиса матрица линейного оператора A также изменится.

Пусть задан базис 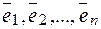в пространстве 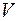и 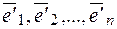- новый базис, а U – матрица перехода от базиса 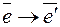, тогда матрица линейного оператора в двух базисах связаны следующим соотношением: 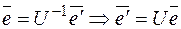, т. к.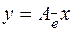 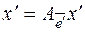, 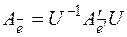и , .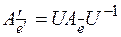

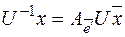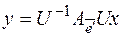Определение. Число λ называется собственным значением если существует ненулевой вектор 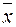такой, что 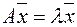, при этом 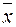называется собственным вектором оператора . Т.к. 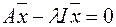, , 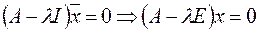тогда чтобы однородная система имела ненулевое решение необходимо и достаточно, чтобы 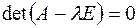. Многочлен 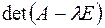называется характеристическим многочленом .

Чтобы найти собственные числа нужно решить уравнение .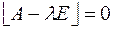

Чтобы найти собственный вектор 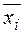, соответствующий собственному числу 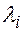необходимо решить систему .

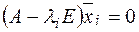1. Каждый линейный оператор имеет собственное значение.

2. Собственные числа и векторы не всегда вещественные.

3. У симметричной матрицы собственные числа всегда вещественны.

4. Собственные векторы соответствующие собственным значениям различные линейно независимы.

5. Если характеристический многочлен n-ой степени оператора имеет n – различных корней, то в некотором базисе матрица оператора A имеет диагональный вид.

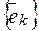6. Для того чтобы матрица A линейного оператора в данном базисе была диагональной, необходимо и достаточно, чтобы базисные векторы 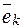были собственными векторами этого оператора.

Определение. Линейный оператор называется самосопряженным, если для любых 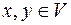выполняется равенство: .

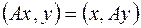Дата добавления: 2013-12-11