Кривые второго порядка

Лекция 17

Свойство самосопряженного линейного оператора

1. Собственные значения самосопряженного оператора вещественны.

2. Если A – самосопряженный оператор, то собственные векторы, отвечающие различным собственным значениям этого оператора ортогональны.

Определение. Квадратичной формой называется однородный многочлен второй степени относительно n переменных 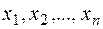. Квадратичную форму всегда можно представить в виде: 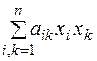, (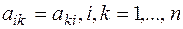), где 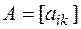- симметрическая матрица (т.е. ).

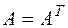Если 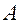– вещественная симметричная матрица, то форма называется вещественной, 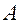– самосопряженная.

В дальнейшем будем рассматривать вещественные квадратичные формы.

Теорема. Для каждой квадратичной формы существует базис, в котором она имеет канонический вид (т.е. представляет сумму квадратов) или такой вид в котором матрица квадратичной формы имеет диагональный вид.

Цель: Изучить канонические уравнения линий второго порядка, их основные характеристики.

Определение. Окружность – это геометрическое место точек равноудаленных от некоторой фиксированной точки называемой центром окружности (рис.17.1).

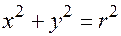(17.1)

если центр перенесен в точку с координатами 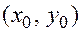, то

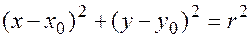(17.2)

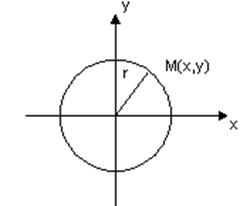
Рис. 17.1

Определение. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости 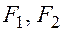, называемых фокусами, есть величина постоянная равная .

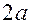Выведем каноническое уравнение эллипса. Возьмем произвольную точку 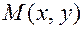, принадлежащую эллипсу. Отрезки 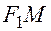, 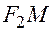называются фокальными радиусами точки и обозначаются 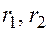(Рис17.2). Их постоянную сумму принято обозначать через 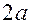. Поэтому

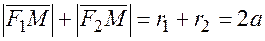(17.3)

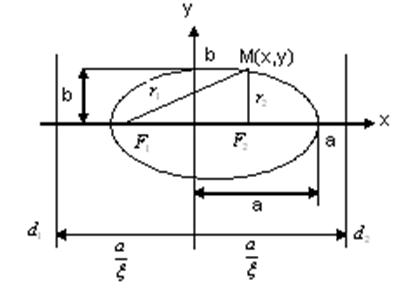
Рис. 17.2

Расстояние между фокусами обозначим за 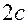и будем называть фокальным расстоянием. При этом 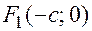, 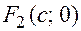. Т.к.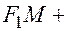 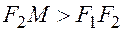, то 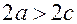и следовательно

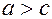(17.4)

Для вывода уравнения выразим фокальные радиусы через координаты точек :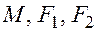

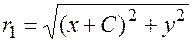
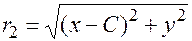
Подставим полученные выражения в формулу (17.3)

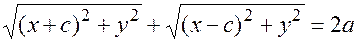и избавимся от корней

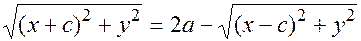возводим в квадрат

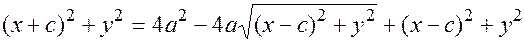
Сокращаем на 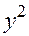, раскрываем скобки

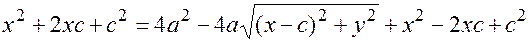сокращаем на 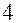, переносим корень влево

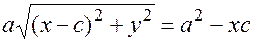
еще раз в квадрат: 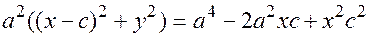раскрываем и группируем

;

.

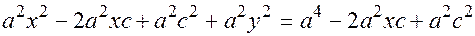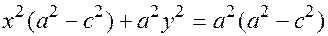В полученном выражении введем обозначение

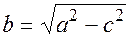(17.5)

Получим каноническое уравнение эллипса 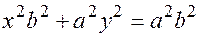или

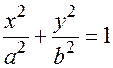(17.6)

Где 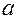- большая полуось эллипса, 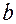- малая полуось эллипса

Из соотношения (17.5) получим формулу для фокального расстояния эллипса:

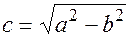(17.7)

Если центр перенесен в точку с координатами 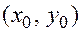, то каноническое уравнение эллипса имеет вид:

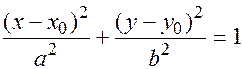(17.8)

Определение. Отношение расстояний между фокусами эллипса и длиной его большой оси. Называется эксцентриситетом и обозначается

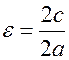(17.9)

Т.к. для эллипса 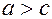, то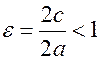

Сократим равенство (17.9) на 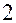и возведя в квадрат выполним следующие преобразования:

,

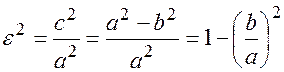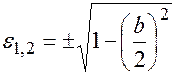или .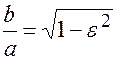

Из последних равенств видно, что эксцентриситет определяется отношением осей эллипса и наоборот, следовательно, чем больше эксцентриситет, тем более вытянута форма эллипса, при уменьшении эксцентриситета – эллипс стягивается в окружность.

Для произвольной точки эллипса , .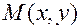

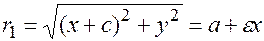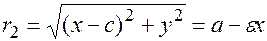Система 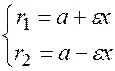определяет параметрическое уравнение эллипса.

В полярной системе координат уравнение эллипса имеет вид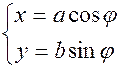

Для эллипса вводят две прямые называемые директрисами, их канонический вид: , .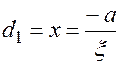

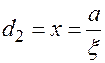Определение. Эллипс - геометрическое место точек, для которых отношение фокального радиуса к расстоянию до соответствующей директрисы равно эксцентриситету эллипса (рис. 17.3):

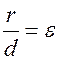(17.10)

Рис.17.3

Определение. Гипербола – это геометрическое место точек, для каждой из которых разность расстояний от двух фиксированных точек плоскости 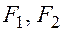, называемых фокусами, есть величина постоянная равная .

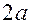Любая точка принадлежит гиперболе, если разность между ее фокальными радиусами равна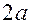(рис.17.3).

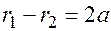(17.11)

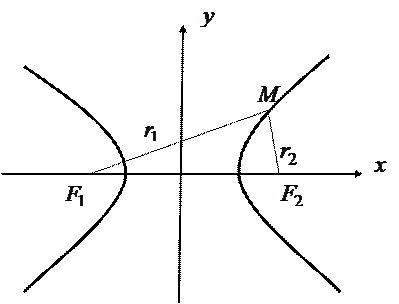
Рис.17.4

поступая по аналогии с выводом уравнения эллипса, получим каноническое уравнение гиперболы

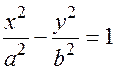(17.12)

Где 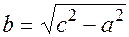, 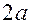- действительная ось, 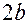- мнимая ось, 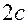- фокальное расстояние.

Расстояние до фокуса гиперболы будет определятся равенством: 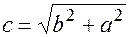(17.13)

Прямые 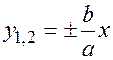(17.14)

называются асимптотами гиперболы.

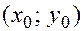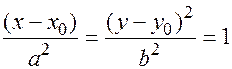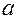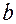Если координаты центра смещены в точку , то каноническое уравнение гиперболы имеет вид (17.15) Прямоугольник, построенный на величинах и – называется основным прямоугольником гиперболы (рис. 17.5).

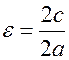
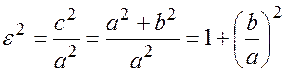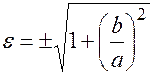Эксцентриситет гиперболы определяется как отношение фокального расстояния к действительной оси

, или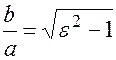

т.е. эксцентриситет гиперболы характеризует форму основного прямоугольника, и следовательно форму гиперболы.

Определение. Две прямые, ортогональные той оси гиперболы, которая ее пересекают и расположенные симметрично относительно центра на расстоянии 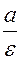от него называются директрисами гиперболы. Обозначаются 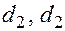(рис.17.5).

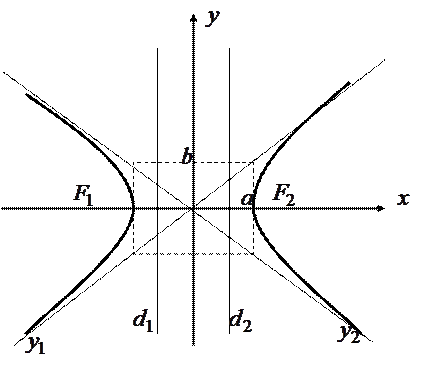Рис.17.5

Определение. Парабола – это геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки 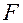, называемой фокусом равно расстоянию до некоторой фиксированной прямой 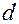, называемой директрисой (рис. 17.6):

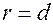(17.16)

Расстояние 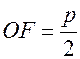– называется фокальным расстоянием параболы, а параметр 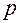- параметром параболы. Т.к. для параболы 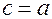, то .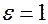

Выведем уравнению параболы, используя формулу (17.16) и то обстоятельство, что , .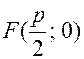

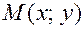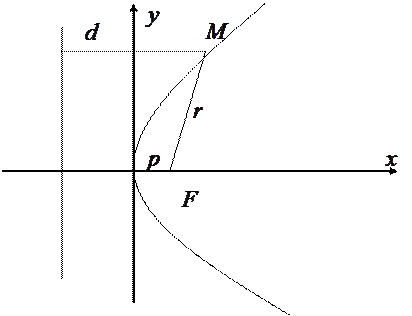Рис. 17.6

, .

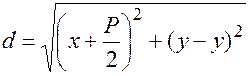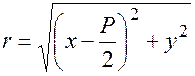Приравниваем 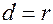и возводим в квадрат:

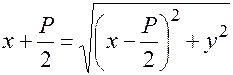
Избавляемся от корня повторным возведением в квадрат

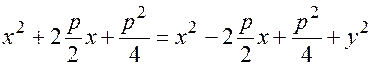
Приходим к каноническому уравнению параболы

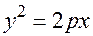(17.17)

Если вершина параболы смещена в точку 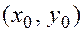, то каноническое уравнение имеет вид: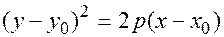

Дата добавления: 2013-12-11