Вычисление площадей плоских фигур

Как уже говорилось выше площадь криволинейной трапеции, расположенной выше оси абсцисс 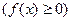, равна определенному интегралу 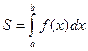или 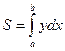. Формула получена путем применения первого способа – метода сумм. Покажем, что именно это можно получить, используя приращение 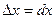. При этом 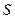получит приращение 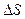, представляющее площадь элементарной криволинейной трапеции. 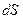в этом случае есть главная часть приращения 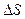при 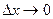и, очевидно он равен произведению 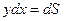, как площади прямоугольника с высотой 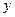и с основанием .

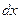Интегрируя полученное соотношение в пределах от 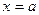до 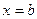, получим 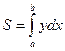. Если криволинейная трапеция расположена ниже оси 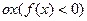, то ее площадь может быть найдена по формуле 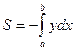. Эти формулы можно объединить в одну 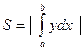. Площадь фигуры, ограниченной двумя кривым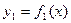и и 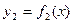(рис.1) при условии 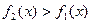и прямыми 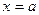; 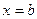можно найти, используя соотношение: 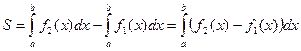. Если плоская фигура имеет сложную форму, то прямыми, параллельными оси 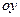ее следует разбить на части так, чтобы можно было применить выше записанные соотношения (рис.2). Если криволинейная трапеция ограничена прямыми 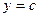, , 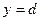осью 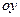и кривой 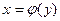, то ее площадь находится по формуле 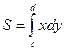. И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически: 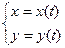, прямыми 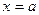, 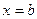и осью 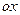, то площадь ее 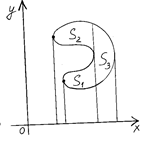находится по формуле: 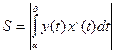, где α и β определяются из равенств 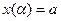и .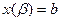

Дата добавления: 2013-12-12