Дифференциальные уравнения высших порядков

ДУ порядка выше первого называются ДУ высших порядков. Так ДУ второго порядка в общем случае записывается в виде следующего соотношения

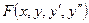
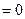
или, если это уравнение можно разрешить относительно старшей производной

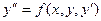(8)

В дальнейшем мы будем, в основном, рассматривать уравнения типа (8). Решением такого уравнения называется всякая функция 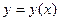, которая при подстановке в уравнение обращает его в тождество.

Общим решением такого ДУ называется функция

,

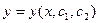где 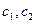независящие от 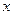постоянные удовлетворяющие условиям:

1) 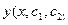является решением ДУ для каждого фиксированного значения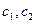

2) каковым бы ни были начальные условия 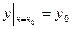, 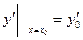существуют единственные значения постоянных 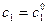и 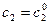такие, что функция 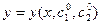является решением уравнения (8) и удовлетворяет начальным условиям.

Всякое решение 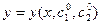уравнения (8) полученное из общего решения 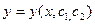при конкретных значениях постоянных 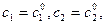называется частным решением.

Решения ДУ (8) записанные в виде 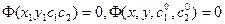называются общим и частным интегралом соответственно.

Как и в случае уравнения первого порядка, нахождение решения (8) удовлетворяющего заданным начальным условиям называется задачей Коши.

Теорема 2. Если в уравнении (8) функция 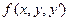и ее частные производные 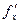и 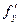непрерывны в некоторой области Д изменения переменных 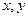и ,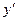

то для всякой точки 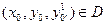существует единственное решение 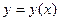уравнения (8) удовлетворяющее начальным условиям.

Аналогичные соображения и понятия можно сформулировать и для ДУ n-го порядка, которое в общем виде можно записать так:

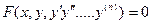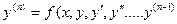или (9)

если его удается разрешить относительно .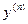

Общим решением ДУ n-го порядка будет являться функция вида 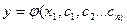содержащей независящие от x постоянные. Начальные условия для ДУ (9) записываются так:

, ,

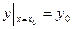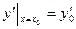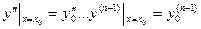
Решение ДУ (9) получающееся из общего решения при конкретных значениях постоянных 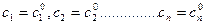называется частным решением. Решить ДУ n-го порядка означает, что найдено его общее или частное решение в зависимости от заданных начальных условий.

Сама задача нахождения решения ДУ n-го порядка гораздо сложнее, чем первого. Поэтому рассмотрим лишь решение отдельных видов ДУ высших порядков.

Дата добавления: 2013-12-12