Решение ЛОДУ второго порядка с постоянными коэффициентами

Решение ДУ второго порядка с постоянными коэффициентами.

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений является ЛОДУ с постоянными коэффициентами. Пусть одно ЛОДУ второго порядка.

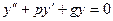(14)

Где p и g – const величины.

Для нахождения общего решения этого уравнения достаточно найти два его частных решения, образующих фундаментальную систему (Теорема 4).

Будем искать частные решения этого уравнения в виде 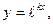где k – некоторое число. Дифференцируя эту функцию два раза и подставляя выражения для 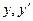и 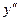в наше уравнение получим

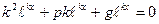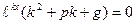т.е. или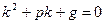

.

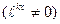Это уравнение называется характеристическим уравнением ДУ (14).Для его составления достаточно заменить в уравнении (14) 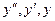соответственно на 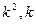и 1.

При решении характеристического уравнения возможны следующие три случая:

1) корн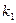и и 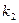уравнения действительны и различны .

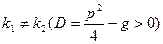В этом случае частными решениями уравнения (14) является функция .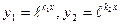

Они образуют фундаментальную систему решений (линейно независимы),следовательно общее решение уравнения (14)в соответствии с формулой (12) имеет вид:

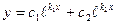(15)

Пример: Решить уравнение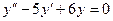

Составим характеристическое уравнение 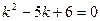, решая его получим 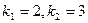.Запишем общее решение данного уравнения 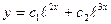, где 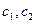- произвольные const.

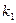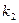2) корни и характеристического уравнения действительные и равные

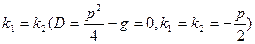.В этом случае имеем лишь одно частное решение

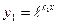.Кроме того можно показать,что наряду с 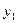решением (14) будет и .

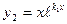Действительно, подставив 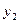в (14) получим: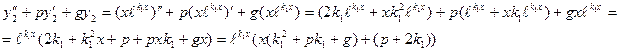

Но 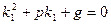т.к. 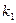- корень этого характеристического уравнения,

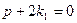т.к. по условию .

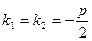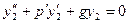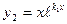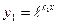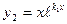Поэтому т.е. является решением уравнения (14).Частные решения и образуют фундаментальную систему решений,следовательно в этом случае общее решение ЛОДУ (14) имеет вид

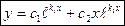(16)

3) корн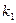и и 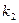комплексные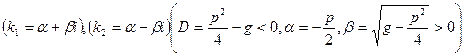
В этом случае частными решениями уравнения (14)являются 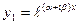и 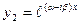.По формуле Эйлера 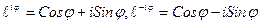тогда имеем

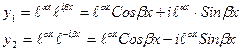(14)

Найдем два действительно частных решения уравнения, для этого составим две линейных комбинации решен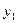ий 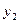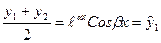и .

и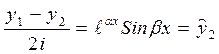

Функци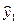и и 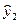являются решениями уравнения (14),что следует из свойств решений ЛОДУ второго порядка (Теорема 3).Эти решения образуют фундаментальную систему решений, так как они являются линейно независимыми. Поэтому общее решение уравнения (14) запишется в виде

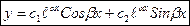(17)

Пример: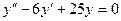

Запишем характеристическое уравнение 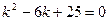, здесь 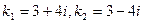, тогда общее решение уравнения примет вид

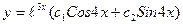
Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (14) сводится к нахождению корней характеристического уравнения и выше полученных формул для общих решений (15),(16),(17) уравнений, не прибегая к вычислению интегралов.

Дата добавления: 2013-12-12