Алгоритм дискретного метода

А) Решение в смешанной форме

Решение полной системы уравнений

Итак, при расчете НДС плоской стержневой системы дискретным методом участвуют четыре вектора:

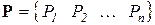– вектор нагрузки;

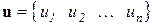– вектор перемещений;

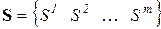– вектор усилий;

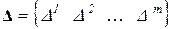– вектор деформаций.

Между этими векторами имеется три зависимости:

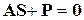– уравнение равновесия; (3)

– геометрическое уравнение; (4)

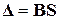– физическое уравнение. (5)

Уравнения (3)-(5) объединяются в общую систему уравнений и называются полной системой уравнений строительной механики. Ее решение дает полную картину НДС всего сооружения.

Систему уравнений (3)-(5) с тремя неизвестными S, u, 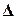можно решать тремя способами.

Для этого правую часть уравнения (5) нужно подставить вместо 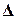в уравнение (4). Тогда останутся два уравнения:

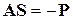, (6)

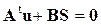. (7)

Объединим их в одно матричное уравнение:

.

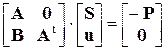Из его решения определяются искомые внутренние усилия и деформации сооружения:

.

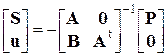Однако из-за большой размерности обращаемой матрицы и ее несимметричности расчет этим способом сложен для реализации.

б) Решение в перемещениях

Для этого из (7) найдем усилия:

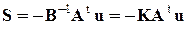, (8)

где обратная к 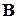матрица 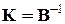называется матрицей жесткости.

Теперь подставим (8) в (6) и получим

.

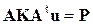Из него определяется вектор перемещений

.

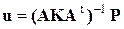Если этот результат подставить в (8), то определяются и усилия.

в) Решение в усилиях

Из-за сложности решения рассматривать его не будем.

1. Ввести в расчетную схему узлы и выбрать расчетную модель.

2. Составить вектор узловых перемещений u.

3. Составить вектора неизвестных усилий S и деформаций .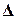

4. Перенести внешнюю нагрузку в узлы.

5. Вырезая узлы, записать уравнения равновесия.

6. Собрать матрицу равновесия A и вектор нагрузки P.

7. Составить матрицы податливости отдельных элементов 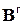и собрать из них матрицу податливости необъединенных элементов B.

8. Решить полную систему уравнений строительной механики. Решение в перемещениях ведется в следующей последовательности:

а) ;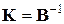

б) ;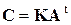

в) ;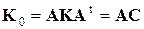

г) ;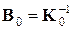

д) ;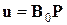

е) ;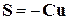

ж) .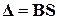

9. По вектору усилий S построить эпюры M, Q, N.

При необходимости по векторам u и 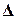можно построить общую картину деформации сооружения.

Дата добавления: 2013-12-12