Переход к общей системе координат

Перенос нагрузки в узлы

РАСЧЕТ СООРУЖЕНИЙ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ (продолжение)

В о п р о с ы

1. Какой из подходов механики реализуется в МКЭ?

2. Какие основные типы КЭ используются в МКЭ?

3. Как формулируется принцип Лагранжа?

4. Для чего нужны координатные функции и матрицы форм?

5. Что такое функция формы?

6. Как определяется матрица жесткости КЭ?

7. Какой физический смысл имеют элементы матрицы жесткости?

Л е к ц и я 15

В расчетной модели сооружения по МКЭ нагрузка должна быть приложена только в узлах. Поэтому действующую на систему внеузловую нагрузку необходимо переносить в узлы.

Порядок переноса нагрузки в узлы расчетной модели в простых случаях остается таким же как и ранее. Например, в стержневых системах используется таблица метода перемещений.

Если к прямоугольному КЭ действует изменяющаяся по линейному закону распределенная нагрузка (рис. 15.1 а), то узловые силы (рис. 15.1 б) определяются по формулам

, .

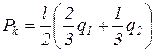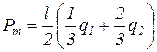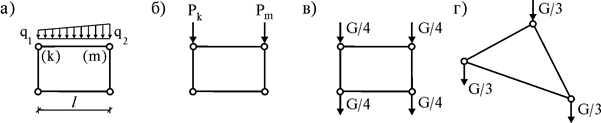
Рис. 15.1

При переносе объемной нагрузки, например собственного веса четырехугольного КЭ, в каждый узел нужно прикладывать четвертую часть его веса G (рис. 15.1 в). При переносе собственного веса треу-гольного КЭ в каждый узел прикладывается его третья часть (рис. 15.1 г).

В общем случае вектор узловой нагрузки определяется по формуле

.

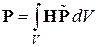Каждый КЭ в МКЭ вначале рассматривается в местной системе координат. Затем осуществляется переход к глобальной (общей) системе координат. Рассмотрим порядок такого перехода.

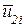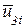Пусть некоторый узел i в местной системе координат имеет перемещения , , , которые следует преобразовать в перемещения узла 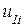, , 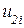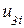в общей системе координат x-y (рис. 15.2 а).

Поворот координатных осей осуществляется с помощью матрицы преобразования координат. Для плоской системы она имеет вид

.

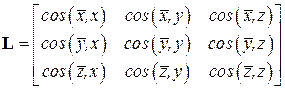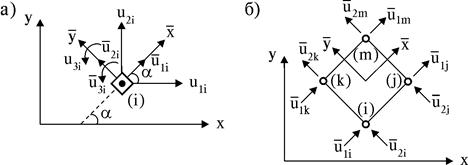
Рис. 15.2

Если координатные системы ортогональны и поворот осуществляется на угол a, то

.

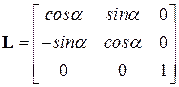Для шарнирного узла с двумя степенями свободы

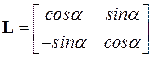. (1)

Эти матрицы позволяют использовать матрицы и вектора геометрических и жесткостных характеристик КЭ, полученных в местной системе координат, для получения соответствующих характеристик КЭ в общей системе координат. Например, преобразование вектора координат прямоугольного КЭ с четырьмя шарнирными узлами i-j-k-m (рис. 15.2 б), рассматриваемогов местной системе координат , в общую систему координат x-y осуществляет матрица

.

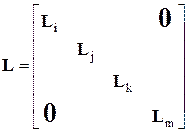Блоки 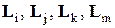этой матрицы имеют вид (1). Имея матрицу жесткости КЭ 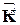в местной системе координат, можно определять ее матрицу жесткости в общей системе координат по формуле

.

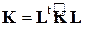Дата добавления: 2013-12-12