Расчетно-графическая работа № 2

Контрольные задания

Вопросы для самоанализа

Выводы

Задача № 2

Задача № 1

Принадлежность точки прямой

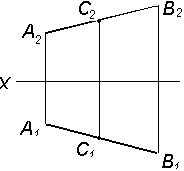Рис. 3.4

Точка принадлежит прямой, если их одноименные проекции совпадают (рис. 3.4). Точка С принадлежит отрезку АВ, так как С2 принадлежит фронтальной проекции отрезка, а С1 – горизонтальной проекции отрезка.

Определить, принадлежит ли точка С отрезку прямой АВ.

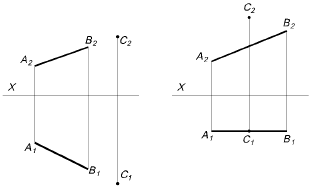
Найти вторую проекцию точки В, если она принадлежит прямой а (рис. 3.12–3.15)

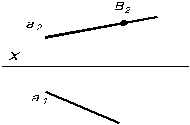
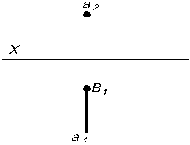
Рис. 3.12	Рис. 3.13
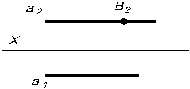
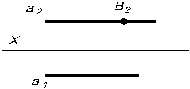
Рис. 3.14	Рис. 3.15

На основе теории Монжа можно преобразовать пространственное изображение не только точки, но и более сложных объектов, в частности прямой линии и ее отрезка.

Для получения проекций отрезка АВ строят проекции его концов-точек А и В – А₁В₁; А₂В₂; А₃В₃. Соединив одноименные проекции точек, получают проекции отрезка А₁В₁ – на плоскость p₁; А₂В₂ – на плоскость p₂; А₃В₃ – на плоскость p₃. Проекции концов отрезков связаны линиями проекционной связи.

Точка принадлежит отрезку, если ее проекции располагаются на одноименных проекциях этой же прямой.

Отрезок прямой относительно плоскостей проекций может быть:

• отрезком общего положения (углы наклона отрезка к плоскостям проекций произвольные);
• отрезком уровня (параллельным какой-либо плоскости проекций);
• проецирующим отрезком (перпендикулярным какой-либо плоскости проекций).

Отрезок может быть задан как в системе p_{1p 2}, так и в p₁p₂p₃.

По двум заданным проекциям всегда можно построить третью.

Отрезок в пространстве характеризуется длиной и углом наклона к плоскостям проекций.

Для отрезков уровня и проецирующих эти величины определяются на самом комплексном чертеже, так как одна из проекций отрезка частного положения есть его натуральная величина.

Для нахождения натуральной величины отрезка общего положения и углов его наклона к плоскостям проекций применяется метод прямоугольного треугольника.

1. Что характерно для прямых, если они параллельны какой-либо плоскости проекции?

2. Какая проекция прямой будет параллельна оси Оx, если эта прямая параллельна p₁?

3. Если одна из проекций прямой есть точка, что это за прямая?

4. Когда прямая проецируется на плоскость в натуральную величину?

5. Как определить натуральную величину отрезка общего положения?

1. Что определяют D z и D y?

Основные понятия, которые необходимо знать:

– проекция прямой, отрезка;

– отрезок общего положения;

– прямые уровня (горизонталь, фронталь, профильная прямая);

– проецирующие прямые (горизонтально проецирующая, фронтально проецирующая, профильно проецирующая прямая).

Способы деятельности, которыми надо уметь пользоваться:

1. Построение третьей проекции отрезка по двум заданным.

1. Нахождение натуральной величины отрезка методом прямоугольного треугольника.

1. Провести сравнительный анализ положения проекций прямых:

а) по расположению относительно плоскостей проекций, осей;

б) по сходству и различию.

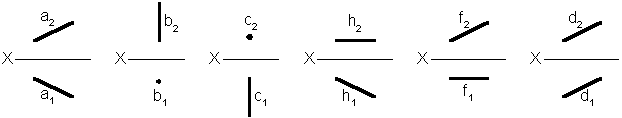
Определение натуральной величины отрезка прямой

Дата добавления: 2013-12-12