Плоскость

Глава 5

Варианты РГР № 3

Вопросы для самоанализа

Выводы

Алгоритм построения прямых параллельных

Вербальная форма	Графическая форма
1. Через точку М провести прямую l || a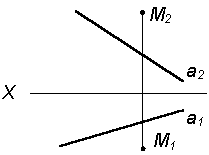
2. Через точку М1 проведем l 1|| a1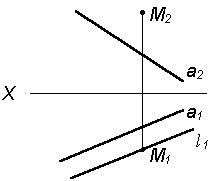
3. Проведем l 2|| a2 через точку М2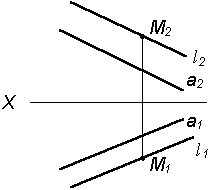

Таким образом, можно сделать следующий вывод: l параллельна а, так как l ₁ параллельна a₁ и l ₂ параллельна a₂.

Прямые в пространстве могут быть:

– пересекающимися;

– параллельными;

– скрещивающимися.

Изображение этих прямых на комплексном чертеже характеризуется расположением их проекций, а именно:

1. если прямые пересекаются в пространстве, то на комплексном чертеже их одноименные проекции пересекаются, а точки пересечения их проекций лежат на одном перпендикуляре к оси проекций;

2. если прямые в пространстве параллельны, то на комплексном чертеже их одноименные проекции параллельны между собой;

3. если прямые скрещиваются в пространстве, то на комплексном чертеже их одноименные проекции пересекаются, но точки их пересечения не лежат на одном перпендикуляре к оси проекций.

Видимость прямых относительно плоскостей проекций определяется с помощью конкурирующих точек.

Используя изученный материал, можно решать на комплексном чертеже такие позиционные задачи, как:

– определять положение прямых и точек относительно друг друга и плоскостей проекций;

– выполнять построение прямых с заданными свойствами (параллельность, пересечение и т.п.).

1. В чем различие положений скрещивающихся и пересекающихся прямых в пространстве?

2. В чем сходство и различие положений проекций пересекающихся и скрещивающихся прямых на комплексном чертеже?

3. Если две прямые в пространстве имеют две общих точки, то они пересекаются. Верно ли это утверждение?

4. Приведите пример положения конкурирующих точек:

– двух скрещивающихся прямых;

– двух параллельных прямых.

5. Сколько проекций надо задать для определения параллельности прямых в пространстве? Рассмотрите варианты решения. Сделайте обобщенный вывод.

Основные понятия, которые необходимо знать:

– параллельность прямых;

– пересечение прямых;

– скрещивание прямых;

– совпадение прямых;

– конкурирующие точки.

Способы деятельности, которыми необходимо владеть:

1. Построение параллельных, пересекающихся, скрещивающихся прямых.

2. Построение прямых, параллельно заданным и построение прямых, пересекающих заданные.

Расчетно-графическая работа № 3
Взаимное положение прямых в пространстве

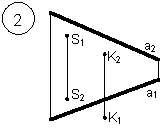
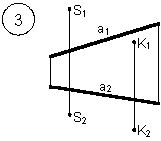
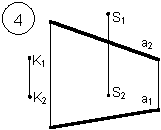
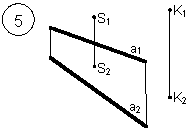
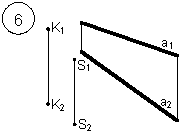
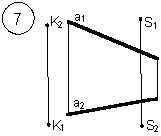
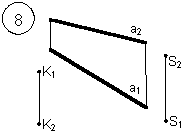
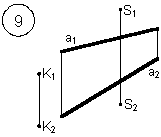
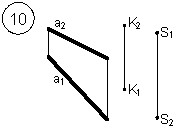
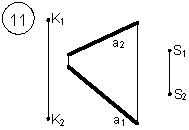
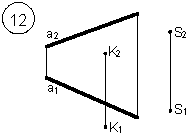
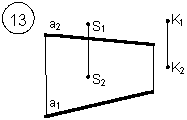
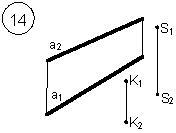
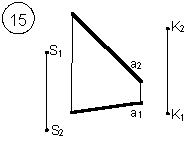
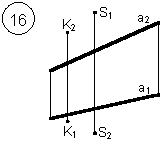
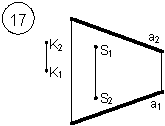
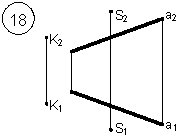
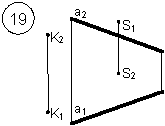
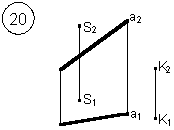
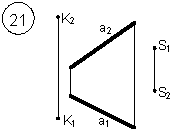
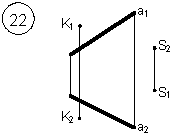
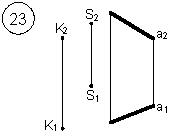
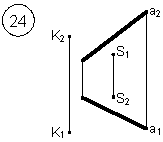
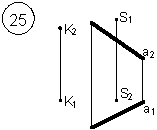
Задания выполняются в соответствии с вариантом.

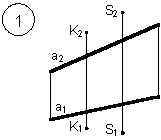
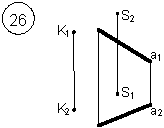
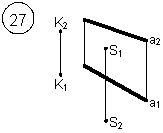
1. Через точку К провести прямую h|| p₁ (четные варианты) или f|| p₂ (нечетные варианты) и прямую l, пересекающую заданную прямую а;

2. Через точку S провести прямую m || a.

Примечание. Образец выполнения расчетно-графической работы № 3 см. прил. 4.

&	[4, гл. 3, § 16–19]; [5, гл. 8, § 46–48]; [6, гл. 3, § 8–10]; [7, гл. 3, подразделы 3.1–3.2]

Дата добавления: 2013-12-12