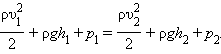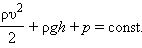Элементы гидро- и аэродинамики

Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 г. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

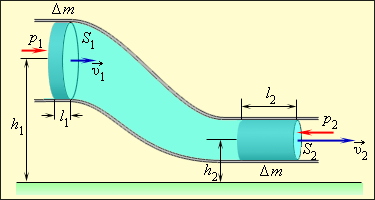
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы могут находиться на разных высотах.

Рисунок 1.22.1. Течение идеальной жидкости по трубе переменного сечения.Δ V ₁ = l ₁ S ₁; Δ V ₂ = l ₂ S ₂. Условие несжимаемости:Δ V ₁ = Δ V ₂ = Δ V

За промежуток времени Δ t жидкость в трубе сечением S ₁ переместится на l ₁ = υ₁Δ t, а в трубе сечением S ₂ – на l ₂ = υ₂Δ t, где υ₁ и υ₂ – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:

Δ V = l ₁ S ₁ = l ₂ S ₂ или υ₁ S ₁ = υ₁ S ₁.

Здесь Δ V – объем жидкости, протекшей через сечения S ₁ и S ₂.

Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.

Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.

При перемещении жидкости силы давления совершают работу:

Δ A = p ₁ S ₁ l ₁ – p ₂ S ₂ l ₂ = p ₁ S ₁υ₁Δ t – p ₂ S ₂υ₂Δ t = (p ₁ – p ₂)Δ V.

Работа Δ A сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.

Изменения, произошедшие за время Δ t в выделенной части жидкости, заключенной между сечениями S ₁ и S ₂ в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δ m = ρΔ V (ρ – плотность жидкости) из одной части трубы сечением S ₁ в другую часть сечением S ₂ (заштрихованные объемы на рис. 1.22.1). Закон сохранения механической энергии для этой массы имеет вид:

E ₂ – E ₁ = Δ A = (p ₁ – p ₂)Δ V,

где E ₁ и E ₂ – полные механические энергии массы Δ m в поле тяготения:

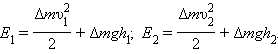
Отсюда следует:

Это и есть уравнение Бернулли. Из него следует, что сумма

остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h ₁ = h ₂) уравнение Бернулли принимает вид:

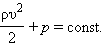
Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1.22.2). Из уравнения Бернулли следует:

Дата добавления: 2013-12-12