Предварительные сведения о процессах теплопередачи

Сохранение энергии

Лекция №2.

Основные выводы.

Итак, применение фундаментального закона сохранения массы позволило получить разнообразные модели рассматриваемых процессов. Различие между моделями определяется типов полученных уравнений (гиперболический, параболический, эллиптический), их пространственно-временными характеристиками (стационарное, нестационарное, одномерное, многомерное), наличием или отсутствием нелинейностей, а также постановкой краевых условий. Таким образом, в зависимости от конкретных свойств объекта и дополнительных предположений, основываясь на одном и том же фундаментальном законе, можно получить совершенно различные математические модели. С другой стороны, одни и те же математические модели могут, в силу своей универсальности, отвечать объектам совершенно разной природы.

Закон сохранения энергии вместе с некоторыми дополнительными предположениями применим для построения моделей распространения тепла в сплошной среде. Сформулируем типичные краевые задачи для уравнений теплопередачи. Обсудим некоторые физические и математические свойства полученных моделей.

Тепловая энергия или тепло – это энергия хаотичного движения атомов или молекул вещества. Обмен теплом между различными участками называется теплопередачей, а сами материалы, обладающие хорошо выраженным свойством теплопередачи, - теплопроводными. К ним относятся, например, металлы, в которых тепловая энергия переносится в основном свободными электронами, некоторыми газами и т.д. Процессы передачи тепла рассматриваются в условиях так называемого локального термодинамического равновесия (ЛТР). Понятие ЛТР для газов вводится при 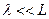, т.е. когда длина свободного пробега частиц вещества много меньше характерных размеров рассматриваемого объекта (сплошная среда). ЛТР подразумевает также, что процессы изучаются при временах, больше чем 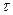(время между столкновениями частиц), и на размерах, больших, чем 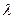. Тогда в областях вещества, размеры которых превосходят величину 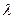(но много меньше величины 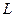), устанавливается равновесие и для них можно ввести средние величины плотности, скорости теплового движения частиц и т.д.

Эти локальные величины (разные в разных точках среды) при сформулированных предположениях находятся из равновесного максвелловского распределения частиц. К ним относится температура 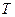, определяющая среднюю кинетическую энергию частиц:

,

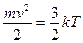где 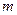– масса частицы, 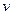- средняя скорость хаотичного движения, 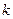- постоянная Больцмана (в случае так называемого больцмановского газа).

Связанная с хаотичным движением частиц энергии вещества (внутренняя энергия) определяется через температуру с помощью величины удельной теплоемкости 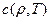, а именно

, ,

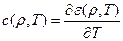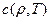где 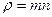– плотность вещества (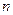- число частиц в единице объема), 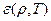- внутренняя энергия единицы массы. Другими словами, теплоемкость – это энергия, которую необходимо сообщить единице массы вещества, чтобы увеличить температуру на один градус.

Наиболее простое выражение для теплоемкости получается в случае идеального газа (газа, частицы которого взаимодействуют лишь при непосредственном взаимодействии столкновения и, подобно биллиардным шарам, без потери суммарной кинетической энергии). Если в некотором объеме идеального газа содержится 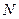частиц, то их полная внутренняя энергия есть

,

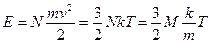где 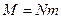- суммарная масса частиц, а удельная внутренняя энергия, или энергия на единицу массы, дается формулой

,

Т.е. теплоемкость идеального газа равна 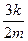и не зависит от величин 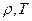. В общем случае связь между внутренней энергией и температурой более сложная. Например, помимо кинетической энергии движущихся частиц, внутренняя энергия содержит составляющую, связанную с потенциальной энергией их взаимодействия, зависящей от среднего расстояния 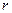между ними. В свою очередь 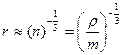, где 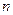- число частиц в единице объема, т.е. 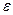зависит от плотности 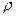. Поэтому в теории теплопередачи величины 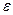(или, что то же самое, 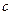) являются, вообще говоря, функциями от 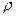и 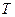. Их конкретный вид определяется свойствами рассматриваемой среды.

Дата добавления: 2013-12-12