Постановка типичных краевых условий для уравнения теплопроводности

Для простоты будем рассматривать одномерные процессы теплопроводности. Они имеют место, например, в длинном и тонком металлическом стержне (рис. 4.1), нагреваемом с одного из торцов, при условии, что стержень изотропен, его начальная температура в любом поперечном сечении не зависит от 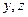(это же свойство должно соблюдаться и на торцах стержня), а потерями тепла с боковой поверхности можно пренебречь. Будем считать также, что теплоемкость стержня постоянна.

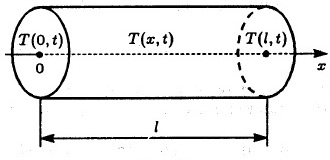
Рис. 4.1

Тогда температура зависит только от 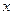и 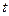, и ее распространение вдоль стержня в различные моменты времени описывается уравнением

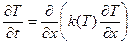, (13)

справедливым при 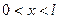, 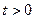. Для определения функции 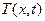, т.е. решения, достаточно задать начальную температуру стержня:

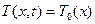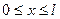, , (14)

и знать температуру на концах стержня в любой момент времени:

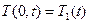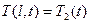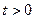, , . (15)

Задача (13) – (15) называется первой краевой задаче для параболического уравнения (13) на отрезке 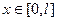. Физически, условие (15) соответствует тому, что на концах стержня с помощью каких-то внешних источников тепла, поддерживается определенная температура, зависящая, вообще говоря, от времени.

Если же на торцах стержня задаются вместо (15) потоки тепла как функции времени:

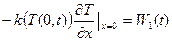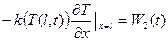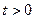, , , (16)

то такая задача называется второй краевой задачей на отрезке 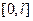. Данная ситуация реализуется, например, когда торцы стержня нагреваются лучами лазерного света известной мощности.

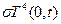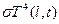Более сложный (нелинейный) вариант условий на торцах отвечает сильно нагретому и поэтому излучающему энергию стержню, не контактирующему с какими-либо телами. Тогда в единицу времени стержень теряет на своих границах (торцах) энергию, равную и соответственно, и вместо (15) или (16) получаются условия

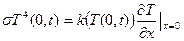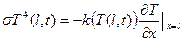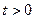, , . (17)

где .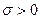

Возможны также и иные виды краевых условий, соответствующие иным физическим ситуациям. Разумеется, допустимы различные комбинации условий (15) – (17), например, на левой конце известна температура, а на правом поток темпа, и т.д.

Разнообразие постановок краевых условий теплопередачи связано с различными идеализациями исходной задачи (13) – (15). При анализе распространения тепла около одного из торцов длинного стержня в течение сравнительно короткого времени влиянием другого торца можно пренебречь. Вместо (15) достаточно задать лишь одно из условий (для определенности на левом конце):

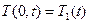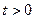, , (18)

и решать уравнения в области 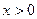((13), (14), (18) – первая краевая задача в полупространстве). Обсуждавшаяся на примере уравнения Буссинеска задача Коши рассматривается во всем пространстве 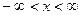. Для уравнения (13) лишь задается начальное распределение температуры (14). Такая постановка вполне разумна, когда рассматриваются процессы в центральной части стержня и влияние обоих торцов можно считать несущественным.

Для многомерных уравнений теплопроводности постановка краевых условий по сравнению с одномерным случаем существенно не меняется: на границах области задаются либо температура, либо поток тепла, либо какие-то более сложные их комбинации, а также (в момент времени 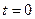) начальное распределение температуры.

Дата добавления: 2013-12-12