Компаундинг

Простая процентная ставка — это ставка, при которой сумма процента начисляется на первоначально вложенную сумму средств; это означает, что сумма процента, начисленного в предыдущие периоды, не принимается в расчет в процессе последующего наращения.

Для простых процентовиспользуются формулы:

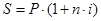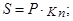или где ;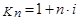

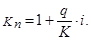
Пример 1. Кредит в размере 10 тыс. руб. выдан 5 августа до 14 ноября под 20% годовых, год високосный. Определить размер наращенной суммы для различных вариантов (обыкновенного и точного) расчета процентов.

Решение. По условию задачи первоначальная сумма (Р) равна 10 тыс. руб, относительная величина простой процентной ставки (i) составляет0,2.

Наращенную сумму определим по формуле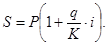

1. В случае точных процентов берем: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 31 день, ноябрь -14 дней. Итого: продолжительность периода начисления процентов составит:

q = 26+30+31+14=101 день.
S = 10 (1 + 101/366 ∙ 0,20) = 10 ∙1,0552 = 10,552 тыс.руб.

2. Для обыкновенных процентов с приближенным числом дней ссуды: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 30 дней, ноябрь -14 дней. Итого: продолжительность периода начисления процентов составит q = 26+30+30+14= 100 дней.

S= 10 (1+100/360 ∙ 0,20) = 10 ∙ 1,0556 = 10,556 тыс.руб.

Ответ: наращенная сумма составит: в случае расчёта точных процентов – 10,552 тыс.руб., для обыкновенных процентов с приближённым числом дней – 10,556 тыс. руб.

Пример 2. Кредит в размере 20 тыс.руб. выдается на 2,5 года. Проценты начисляются один раз в конце срока, но ставка процентов за первый год - 30%, а за каждое последующее полугодие она уменьшается на 1%. Определить множитель наращения и наращенную сумму.

Решение. По условию задачи первоначальная сумма (Р) равна 20 тыс.руб.; продолжительность периода начисления процентов в годах (n) составляет 2,5 года; относительные величины простых процентных ставок (i) по периодам начисления составят: за два полугодия первого года - i₁= 0,3; за первое полугодие второго года - i₂= 0,29; за второе полугодие второго года - i₃ =0,28; за первое полугодие третьего года - i₄ =0,27.

1. Используем формулу для определения множителя наращения при различных процентных ставках на разных интервалах

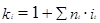; к_н = 1 + 0,3 + 0,5 (0,29 + 0,28 + 0,27) = 1,72.

2. Используем формулу для определения наращенной суммы при заданном множителе наращения: S = P x k_н.

S = 20 x 1,72 = 34,4 тыс.руб.

Ответ: множитель наращения равен 1,72, а наращенная сумма – 34,4 тыс.руб.

Пример 3. Определить период начисления, за который первоначаль-ный капитал в размере 25000 руб. вырастет до 40000 руб., если используется простая ставка 28 процентов годовых.

Решение. По условию задачи наращенная сумма (S) составляет 40000 руб., а первоначальная (P) - 25000 руб.; относительная величина простой процентной ставки (i) составит 0,28.

По формуле для определения периода начисления: 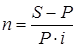получаем: 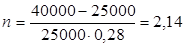года.

Ответ: период начисления составит 2,14 года, т.е. 2 года и 2 месяца.

Пример 4. Определить простую ставку процентов, при которой первоначальный капитал в размере 24000 руб. достигнет 30000 руб. через год.

Решение: По условию задачи величина первоначальной денежной суммы (P) составляет 24000 руб.; наращенной суммы (S) - 30000 руб., продолжительность периода начисления процентов в годах (n) - 1 год.

По формуле для определения относительной величины простой процентной ставки 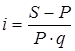определяем: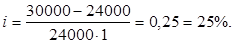

Ответ: простая процентная ставка составит 25% годовых.

Сложная процентная ставка — это такая ставка, при которой процент начисляется на постоянно нарастающую базу с учетом процентов, начисленных в предыдущие периоды («проценты на проценты»):

Для сложных процентов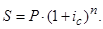

Множитель наращения k_н.с. соответственно будет равен

k_н.с. = (1 + i_c) ⁿ.

Если срок ссуды n в годах не является целым числом, множитель наращения определяют по выражению: k_н.с. = (1 + i_c) ^nа (1+ n_b i_c), где

n = n _а + n _ь;

n _а – целое число лет;

n _ь – оставшаяся дробная часть года.

Пример 5. Первоначальная сумма долга (Р) равна 50 тыс.руб. Определить наращенную сумму (S) через 2,5 года по ставке 25% годовых.

Дата добавления: 2013-12-12