Решение. Эквивалентность процентных ставок различного типа

Эквивалентность процентных ставок различного типа

Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты.

Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.

Приравнивая соотношения 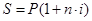и 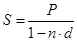, получим:

– простая годовая ставка ссудного процента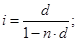

– простая годовая учётная ставка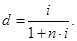

Пример 11. Срок уплаты по долговому обязательству – полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?

Используем формулу простой годовой ставки ссудного процента

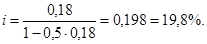
Проверка: 1. При простой процентной ставке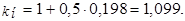

2. При простой учётной ставке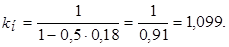

Пример 12. Определить, под какую ставку процентов выгоднее поместить капитал на два года:

а) под простую ставку процентов 20% годовых;

б) под сложную ставку в 16% при ежеквартальном начислении?
Решение

I способ. Найдём простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой:

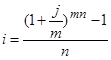. , т.е. 18,43%.

Так как простая процентная ставка (20%), которая дала бы одинаковый с данной сложной процентной ставкой результат, превышает предложенную (18,43%), ясно, что выгоднее использовать простую процентную ставку.

II способ. Посчитаем коэффициенты наращения, получаемые в обоих случаях: а) под простую ставку процентов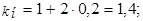

б) под сложную ставку при ежеквартальном начислении

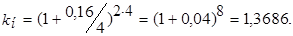
Разница в результатах подтверждает сделанный ранее вывод.

Дата добавления: 2013-12-12