Аннуитет постнумерандо

Аннуитеты

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Такая последовательность называется потоком платежей.

Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют аннуитетом, или финансовой рентой.

Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) – пожалуй, самый распространенный случай. Такой аннуитет предполагает получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода (года, полугодия, квартала, месяца и т.д.).

Введем следующие обозначения:

Р –величина каждого отдельного платежа;

i_с – сложная процентная ставка, по которой начисляются проценты;

S_k – наращенная сумма для k-го платежа аннуитета постнумерандо;

S – наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);

A_k – современная величина к-го платежа аннуитета постнумерандо;

А –современная величина всего аннуитета постнумерандо.

п – число платежей.

Аннуитет постнумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c.

Основные количественные характеристики аннуитета постнумерандо:

1. Общая наращенная сумма определяется по формуле:

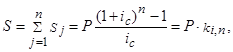
где k_i,n – коэффициент наращения в удобном для вычислений виде равен: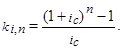

Для определения коэффициентов наращения и приведения обыкновенного аннуитета существуют таблицы, которыми удобно пользоваться в практических вычислениях. Нужно иметь в виду, что n в данном случае – не число лет, а число периодов одинаковой продолжительности (день, месяц, квартал и т. д.), в которых принята данная процентная ставка. Таким образом, если задана годовая процентная ставка, можно найти эквивалентную ей ставку на более коротком интервале и рассматривать далее п как число таких интервалов.

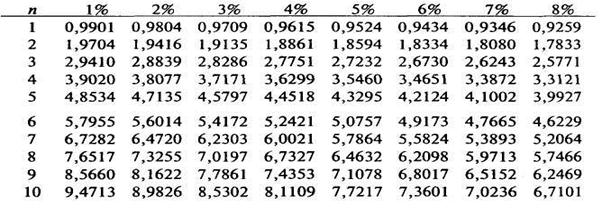
Таблица 3. Коэффициенты наращения аннуитета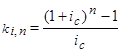

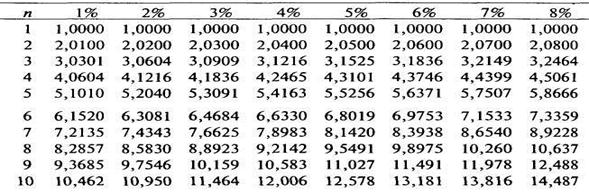
Таблица 4. Коэффициенты приведения аннуитета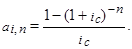

_____________________________________________________________

2. Современная величина всего аннуитета определяется по формуле

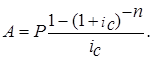
3. Современные значения каждого платежа (А_к) определяются по формуле:

Пример 13. Для погашения пакета облигаций, выпущенных ОАО «Интерком» на 5 лет, создаётся выкупной фонд. Ежегодные платежи предприятия в него составляют 150 000 руб., на них в конце каждого года начисляются проценты по ставке 7 %. Определите итоговую наращенную сумму денежных средств, современную величину всего аннуитета и современное значение каждого платежа.

Решение. Для расчёта будущей стоимости выкупного фонда используем формулу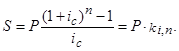

Коэффициент наращения определим по формуле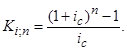

Аналогичный результат получим по таблице. Итоговая наращенная сумма будет равна S = P ∙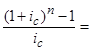150 000 ∙ 5,7507 = 862605 руб.

Современную величину всего аннуитета определим по формуле

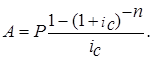
Размер очередного платежа может быть определён по формулам:

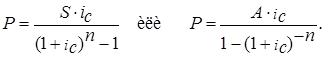
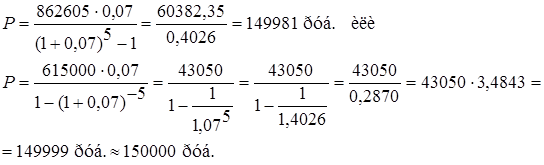
Современные значения каждого платежа (А_к) определим по формуле:

В аннуитете постнумерандо платежи и начисление процентов производится в конце года. Поэтому современная величина платежа за первый год будет равна:

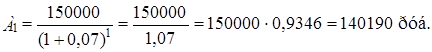
Аналогичным образом произведём дисконтирование платежей за остальные годы.

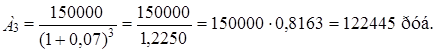
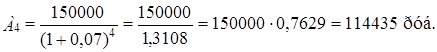
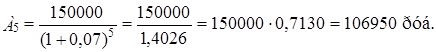
Современная величина всего аннуитета должна быть равна сумме современных значений всех платежей и начисленных процентов, т.е.

А = А₁+ А₂+ А₃+ А₄+ А₅.

В нашем примере

А = 140190+131010+122445+114435+106950=615030 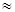615000 руб., что соответствует значению, определённому ранее по формуле.

Ответ: Полный набор показателей аннуитета составил:

- наращенная сумма денежных средств - 862605 руб.;

- современную величину всего аннуитета – 615000 руб.;

- современное значение каждого платежа: А₁ - 140190 руб.; А₂ -131010 руб.;

А₃ -122445 руб.; А₄ – 114435 руб.; А₅ - 106950 руб.

Дата добавления: 2013-12-12