Решение. Аннуитет пренумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке ic

Аннуитет пренумерандо

Аннуитет пренумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c.

Очевидно, отличие от предыдущего случая состоит здесь в том, что период начисления процентов на каждый платеж увеличивается на один год, т. е. каждая наращенная сумма S_k увеличивается в (1 + i_c) раз. Следовательно, для всей суммы S_n имеем S_n =S( 1 + i_c).

Для коэффициента наращения аннуитета пренумерандо 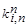получаем следующее соотношение: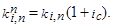

Для определения современных значений каждого платежа дисконтирование по заданной ставке i_c проводится на один раз меньше, чем в случае аннуитета постнумерандо. Поэтому каждая современная величина А_к будет больше в (1+ i) раз. Таким образом, А_п = А(1 + i_c).А для коэффициента приведения a _i,n ^п получаем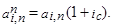

Пример 14. Найти наращенную сумму аннуитета и современную величину потока платежей, если в течение трёх лет доход, получаемый в начале года, будет составлять по 500 тыс.руб. Ставка дисконтирования – 6% годовых.

В данном примерепоток платежей в течение трёх лет представляет собой постоянный аннуитет пренумерандо. Наращенная сумма такого аннуитета определится по формуле:

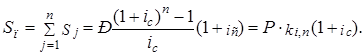
Коэффициент наращения может быть определён по таблице 3 наращенного значения аннуитета: k_{0,06; 3} = 3,1836∙(1+0,06)=3,3746.

Наращенная сумма аннуитета составит:

S^п =500∙3,3746=1687,3 тыс.руб.

Для проверки определим сумму наращенных сумм по годам.

Доход, полученный в первом году, через три года составит:

S₁=500∙(1+0,06)³=500∙1,1910=595,5 тыс.руб.; доход, полученный во втором году, S₂= 500∙(1+0,06)² = 500∙1,1236 = 561,8 тыс.руб. и доход, полученный в третьем году, S₃ = 500∙(1+0,06)¹=500∙1,06 = 530 тыс.руб.

Общая наращенная сумма S^п=S₁^п+S₂^п+S₃^п=595,5+561,8+530=1687,3 тыс.руб.

По формуле 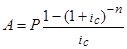(1+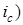можем рассчитать современную величину аннуитета. Коэффициент приведения аннуитета определим по таблице 4. Для n =3 и i_c =0,06 k_{0,06; 3} =2,6730. Тогда kⁿ =2,6730∙1,06=2,8334.

Современная величина аннуитета А^п=500∙2,8334=1416,7 тыс.руб.

Можем проверить вычисления определив сумму современных величин всех платежей и начисленных процентов. Формула современных значений каждого платежа (А_к) примет вид: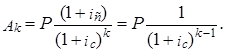

Современные величины всех платежей будут равны:

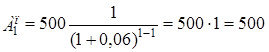тыс.руб.;

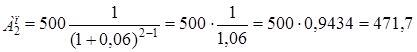тыс.руб.;

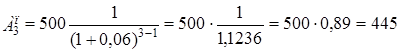тыс.руб.

Сумма современных величин всех платежей будет равна:

А^п = 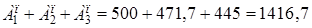тыс.руб.

Ответ: наращенная сумма аннуитета составит 1687,3 тыс.руб., а современная величина аннуитета составит 1416,7 тыс.руб.

Цель вложения денежного капитала в различного вида ценные бумаги – получение дохода и/или сохранение капитала от обесценения в условиях инфляции. Следовательно, необходимо уметь правильно оценивать реальный доход по разного вида ценным бумагам.

Дата добавления: 2013-12-12