Оценка и показатель качества по ВЧХ ЗАС

Частотные оценки

Оценка качества по АЧХ ЗАС

согласно прошлой лекции

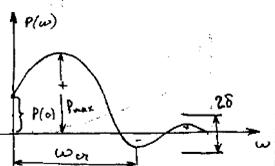Свойства:

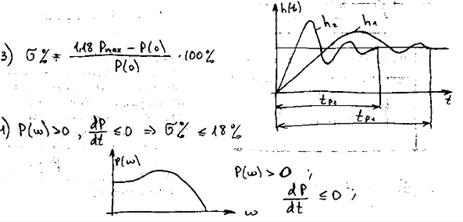
1. Ч ем больше max и min имеет ВЧХ ЗАС, тем больше колебательность ЗАС.

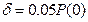
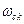-диапазон частот, определяемый частотой, на которой кривая ВЧХ входит входит в полосу 2 дельта и далее из нее не выходит

2.Чем больше диапазон существенных частот тем меньше времени приходится на переходной процесс (чем выше 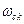, тем выше быстродействие АС)

1. Интегральные оценки качества переходного процесса.

3) Интегральные оценки кач-ва

Дают оценку в целом, т.е. на всем интервале времени.

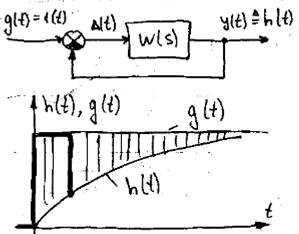
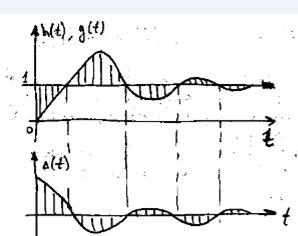
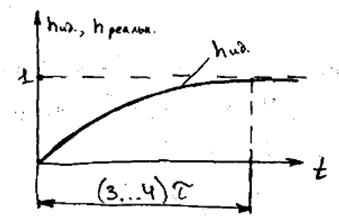
Очевидно, чем меньше площадь между ступенью входного сигнала и переходной функцией, тем лучше переходной процесс, т.е. тем ближе он к идеальному(если за идеальный переходной процесс взять ступенчатую функцию)

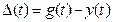
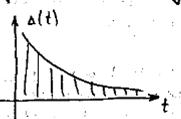
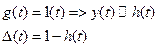
Иначе можно сказать: чем меньше площадь под кривой ошибки тем ближе переходной процесс к идеальному. Площадь под кривой можно определить как интеграл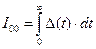

Таким образом получаем линейную интегральную оценку. Чем меньше 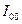тем ближе переходной процесс к идеальному.

Определим 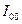при наличии структуру ЗАС.

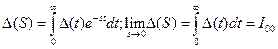
Определим образ ошибки, вспомнив ПФ для нее:

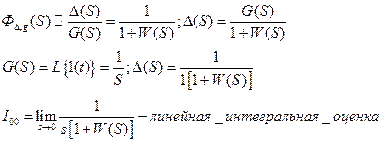
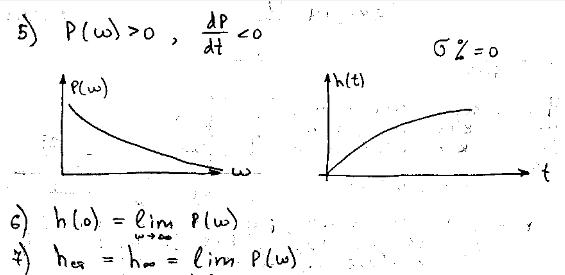
Недостаток линейной интегральной оценки- она плохо работает в случае переходных колебательных процессов.

При определении + и – площади компенсируются. Разным переходным процессам могут соответствовать близкие значения интегральной оценки.

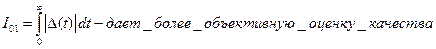
Справедливо для колебательных и других переходных процессов. (я про рис справа)

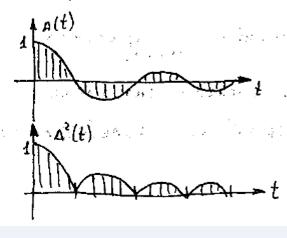Недостаток данной интегральной оценки: Отсутствие аналитичности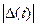в точках пересечения 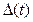с осью времени (т.е. производные слева и справа отличаются по знаку). Наиболее широкое распространение получила интегрально квадратичная оценка(слева рис)

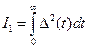. Все интегральные оценки являются функционалами. Функционал- преобразователь функции в число.

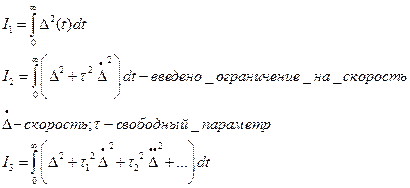
Функция 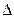, доставляющая минимальное значение интегральной оценки (функционала) называется экстремалью.

Очевидно, что экстремаль будет описывать идеальный переходной процесс. Идеальным переходным процессом можно распоряжаться путем выбора тау. Найдем экстремаль для интегральной оценки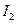

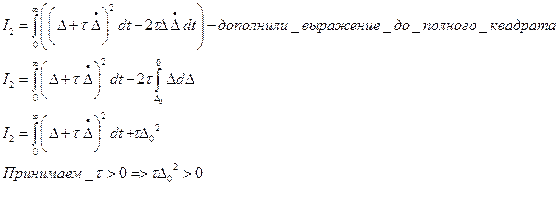
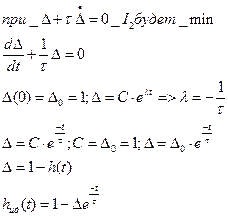
Задавая тау, можем менять идеальный переходной процесс.

Пусть нами определена интегральная оценка I2, как функция параметров системы (А, В). Необходимо найти параметры А и В, при которых оценка будет минимальной

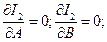
1. Точность АС. Вычисление ошибок по отношению к задающему воздействию. Структурный признак астатизма по отношению к задающему воздействию.

Точн ость АС определяется ошибкой. Типовую структуру АС представим в виде

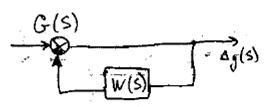
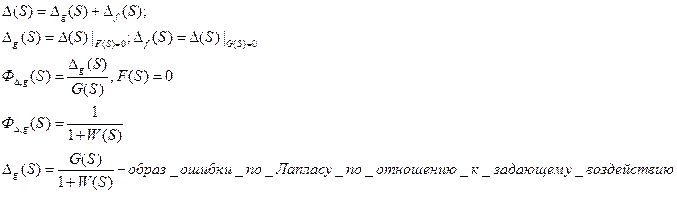
Для определения ошибки от возмущающего воздействия F(S) вспомним ПФ ЗАС для ошибки.

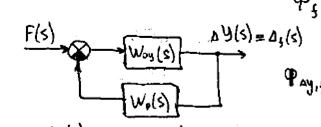
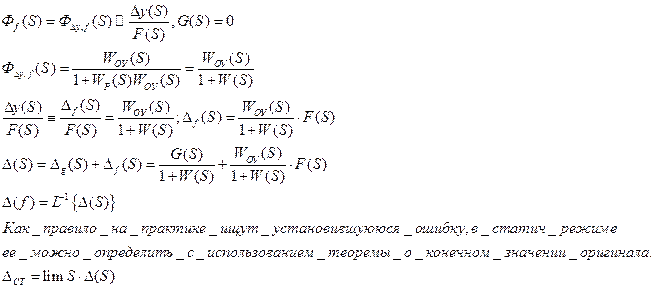
Ошибка зависит от структуры РАС и вида внещнего воздействия.

Дата добавления: 2013-12-12