
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Фазовая плоскость. Свойства фазовой плоскости
|
|
|
|
Пример 2
Пример 1
Пусть имеется нелинейная система с неустойчивым положением равновесия и находится в колебательном режиме.
Известно что энергия диссипации за период, как правило, увеличивается с увеличением амплитуды колебаний.
Наступит момент, когда энергия диссипации за период станет равной энергии подкачки и амплитуда перестанет расти, т.е. наступит автоколебание.
Пусть имеем источник питания для нелинейной системы с насыщением по мощности и пусть имеем так же имеем нелинейную систему с неустойчивым положением равновесия и с колебательным режимом.
Амплитуда колебаний будет возрастать. Наступит момент, когда энергия подкачки будет максимальна.(ограничена)
Автоколебания удобно рассматривать на энергетических диаграммах, которые позволяют определить амплитуду колебаний и их устойчивость.
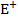 - энергия подкачки за период
- энергия подкачки за период
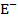 - энергия диссипации за период
- энергия диссипации за период
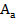 - амплитуда автоколебаний
- амплитуда автоколебаний
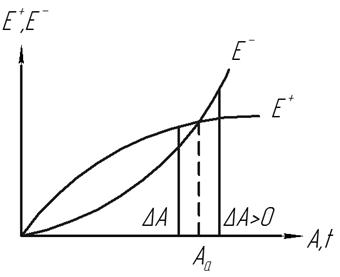
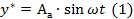
Примем (1) за невозможное движение 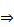 А можно считать мерой начальных условий
А можно считать мерой начальных условий
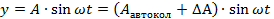 (2)
(2)
Выражение (2) это возмущенное движение
а) 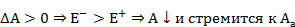
б) 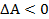
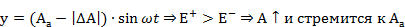 устойчива
устойчива
Кроме автоколебаний открыто новое важное свойство нелинейной системы: возникновение хаотических колебаний
В нелинейных системах устойчивость зависит от типа внешних воздействий (от вида входного сигнала или возмущения)
Вспомним доказательство которое мы делали при исследовании устойчивости нелинеаризованных АС.
Кроме того устойчивость нелинейной АС зависит от положения нелинейной системы, т.е. от начальных условий.
- Фазовое пространство и его смысл для анализа нелинейных АС. Фазовая плоскость. Свойства фазовых траекторий.
Фазовое пространство — пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Смысл фазового пространства ва.
Пусть имеем систему вида 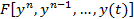 =0(1)
=0(1)
Систему 1 или ДУ назовем автоколебательной системой, т.к. в ней явно отсутствует время и внешнее воздействие.
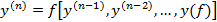 (2)
(2)
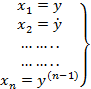 (3)
(3)
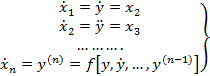 (4)
(4)
На основании 3 получим:
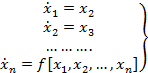 (5)
(5)
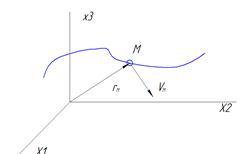
Будем трактовать 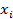 как координату некоторой точки с координатой
как координату некоторой точки с координатой 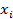
С течением времени эта точка описывает кривую, которую назовем фазовой траекторией.
Будем называть отображающей точкой М
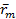 – фазовый вектор
– фазовый вектор
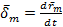 - фазовая скорость
- фазовая скорость
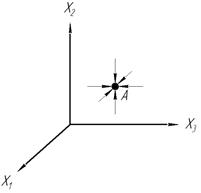 Смысл фазового пространства. По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Смысл фазового пространства. По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Пусть все фазовые траектории стягиваются в точку
Точка А является положением равновесия, причем она устойчива.
Пусть в точку А, в которую входят все траектории можно назвать аттрактор.
Положением равновесия м.б. целой областью – аттрактором.
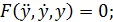 (1)
(1)
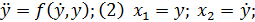 (3)
(3)
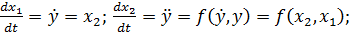 (4)
(4)
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 777; Нарушение авторских прав?; Мы поможем в написании вашей работы!