Пропорции в композиционной структуре произведения искусства

ПОСЛЕДСТВИЯ ПЕРЕДАЧИ НЕДВИЖИМОСТИ

НЕНАДЛЕЖАЩЕГО КАЧЕСТВА

применяются правила ст.475 ГК РФ

(последствия передачи товара ненадлежащего качества (?!) -

кроме положений о праве покупателя потребовать замены товара)

Принятие покупателем недвижимости, не соответствующей условиям договора, в том числе, когда такое несоответствие оговорено в документе о передаче недвижимости, не является основанием для освобождения продавца от ответственности за ненадлежащее исполнение договора

ОСОБЕННОСТИ ПРОДАЖИ ЖИЛЫХ ПОМЕЩЕНИЙ

1. Существенные условия договора

- предмет

- цена

- перечень лиц, сохраняющих в соответствии с законом право пользования жилым помещением после его приобретения покупателем, с указанием их прав на пользование продаваемым жилым помещением

2. Договор государственной регистрации и считается заключенным с момента такой регистрации

Еще в глубокой древности человеком было обнаружено, что все явления в природе связаны друг с другом, что все пребывает в непрерывном движении, изменении, и, будучи выражено числом, обнаруживает удивительные закономерности.

В Древней Греции эпохи классики возник ряд учений о гармонии. Из них наиболее глубокий след в мировой культуре оставило Пифагорейское учение. Последователи Пифагора представляли мир, вселенную, космос, природу и человека как единое целое, где все взаимосвязано и находится в гармонических отношениях. Гармония здесь выступает как начало порядка — упорядочивания хаоса. Гармония присуща природе и искусству: «Одни и те же законы существуют для музыкальных ладов и планет». Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено; что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание). Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что в основе мироздания лежат симметричные геометрические формы.

Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую «Дорифор (Канон)». Все классическое искусство Греции носит печать пифагорейского учения о про порциях. Его влияние испытали на себе ученые средневековья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневековый ученый Августин назвал красоту «числовым равенством». Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: «Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона познает ученый».

Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.

Пропорция означает равенство двух или нескольких отношений. Существует несколько видов пропорциональности: математическая, гармоническая, геометрическая и др. В математической равенство двух отношений выражается формулой a:b=с:d, и каждый член ее может быть определен через остальные три. В гармонической пропорции 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например: а:с=(а — в): (в — с).

В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с. Разновидностью геометрической пропорции является пропорция так называемого «золотого сечения», имеющая всего два члена — «а» и «в» — излюбленная пропорция художников, которую в эпоху Возрождения называли «божественной пропорцией».

Золотое сечение (з. с.) Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е. а:в = в: (а — в). Отношение золотого сечения выражается числом 0,618. Пропорция золотого сечения 1:0,618=0,618:0,382.

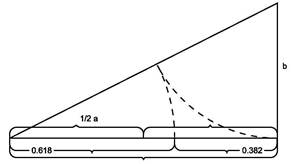
Если, отрезок прямой выразить через единицу, а затем разделить его на два отрезка по золотого сечения, то больший отрезок будет равен 0,618, а меньший 0,382. На рис. 1 показано деление отрезка на части по золотому сечению.

На основании пропорции золотого сечения был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к О,б18, то есть, к отношению золотого сечения.

Рисунок 1. Деление отрезка по золотому сечению

Пропорции золотого сечения ученые связывают с развитием органической материи. Золотое сечение было обнаружено в объектах живой природы — в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его наблюдали в устройстве вселенной в расположении планет. В отношении з. с. находятся так же элементы геометрических фигур — пятиугольника, звезды (рис. 2.).

Рисунок 2. Точки пересечения линий, составляющих звезду,

делят их на отрезки в отношении золотого сечения.

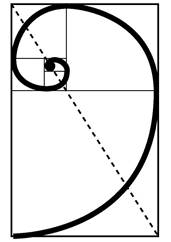В прямоугольнике золотого сечения стороны находятся в отношении золотого сечения. Этот прямоугольник содержит в себе квадрат и малый пр-к золотого сечения (его большая сторона является малой стороной первоначального пр-ка.) Поэтому можно построить пр-к з.с. на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится пр-к золотого сечения. Иначе говоря, если отсечь от прямоугольника золотого сечения квадрат, то остается меньший пр-к, стороны которого опять же будут находиться в отношении золотого сечения. Разбивая этот меньший пр-к на квадрат и еще меньший пр-к, мы опять получим пр-к золотого сечения, и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют «кривая развития», «спираль жизни», ибо в ней как бы заложена идея бесконечного развития (рис. 3).

Дата добавления: 2013-12-12