И направление самопроизвольных процессов

Термодинамические потенциалы

Абсолютное значение энтропии газа.

Абсолютная значение энтропии газа рассчитывается:

,

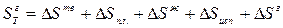где Δ S^ж – изменение энтропии жидкости при нагревании ее от Т _пл. до температуры кипения Т _кип.; Δ S_исп – изменение энтропии при испарении жидкости; Δ S^г – изменение энтропии при нагревании газа от Т _кип до температуры Т. Тогда

.

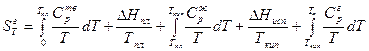Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных: если в результате расчета окажется, что D S > 0, процесс пойдет самопроизвольно, при D S = 0 – состояние равновесия, если D S < 0, процесс самопроизвольно протекать не будет.

На практике приходится иметь дело преимущественно с системами, взаимодействующими с окружающей средой. В качестве критерия оценки направления самопроизвольных процессов в таких системах используются термодинамические потенциалы.

Термодинамическим потенциалом называют функцию состояния, убыль которой в обратимо протекающем процессе при постоянстве определенных параметров равна максимальной полезной работе.

Наибольшее значение имеют два основных термодинамических потенциала: энергия Гельмгольца F (T, V) и энергия Гиббса G (T, p). В скобках указаны параметры, функциями которых являются термодинамические потенциалы.

Чтобы получить представление о термодинамических потенциалах, воспользуемся объединенным математическим выражением первого и второго законов термодинамики.

.

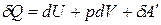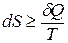или .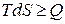

,

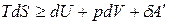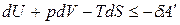. (1.23)

Рассмотрим соответствующие процессы.

И з о б а р н о – и з о т е р м и ч е с к и й п р о ц е с с (p, T = const).

Уравнение (1.23) запишется

,

,

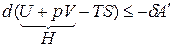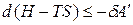где H – TS = G –свободная энергия Гиббса. При p, T = const изменение энергии Гиббса связано с выполнением полезной работы:

.

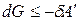В обратимо протекающем процессе 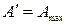. Тогда

,

.

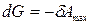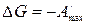Таким образом, свободная энергия Гиббса является изобарно-изотермическим потенциалом, так как ее уменьшение характеризует максимальную работу этого процесса.

Если единственным видом работы является работа расширения (сжатия), т.е. 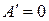, то в необратимом, а, следовательно, самопроизвольно протекающем процессе

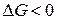. (1.24)

И з о х о р н о – и з о т е р м и ч е с к и й п р о ц е с с (V, T = const).

Уравнение (1.23) примет вид

,

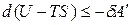где U – TS = F – свободная энергия Гельмгольца. При V, T = const изменение энергии Гельмгольца связано с выполнением полезной работы:

.

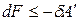В обратимо протекающем процессе

,

.

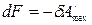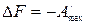Таким образом, свободная энергия Гельмгольца является изохорно-изотермическим потенциалом.

Если 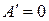, то в самопроизвольно протекающем процессе

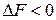. (1.25)

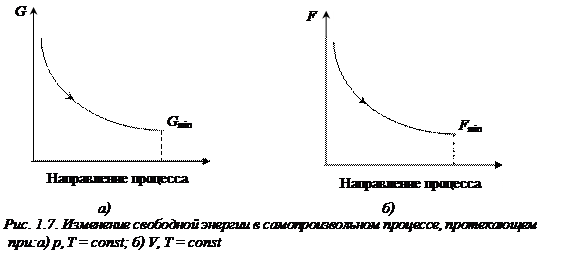
Неравенства (1.24), (1.25) являются условием самопроизвольного протекания процесса при постоянстве соответствующих параметров: самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения (рис. 1.7.).

Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой.

Изменение соответствующего термодинамического потенциала в ходе какого-либо процесса, протекающего при температуре Т, вычисляют по уравнению Гиббса-Гельмгольца:

– для изобарно-изотермического процесса

D G = D H – T D S, (1.26)

– для изохорно-изотермического процесса

D F = D U – T D S. (1.27)

Основываясь на уравнении Гиббса-Гельмгольца (1.26), (1.27), можно оценить вклад энтальпийного и энтропийного факторов в величину Δ G (или Δ F) и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов.

1. Экзотермические реакции, Δ H < 0.

Если Δ S > 0, то Δ G всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.

Если Δ S < 0, реакция будет идти самопроизвольно при D H > T D S (низкие температуры).

2. Эндотермические реакции, Δ H > 0.

Если Δ S > 0, процесс будет самопроизвольным при D H < T D S (высокие температуры).

Если Δ S < 0, то Δ G всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.

Термодинамические потенциалы могут играть роль характеристических функций. Это значит, что с помощью их производных можно выразить свойства системы, необходимые для ее характеристики.

Изобарно-изотермический потенциал является функцией двух параметров – давления и температуры, т.е.

.

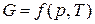Запишем dG в виде суммы частных производных

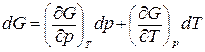. (1.28)

Учитывая, что

,

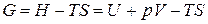получаем:

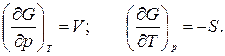
Изохорно-изотермический потенциал является функцией объема и температуры, т.е.

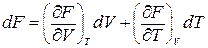. (1.29)

По определению

,

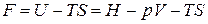откуда следует, что

.

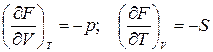Легко установить связь между D G и D F. Вычитая из уравнения (1.26) уравнение (1.27), и учитывая, что D U = D Н – D nRT, получим:

D G = D F + D nRT.

Разберем физический смысл изобарно-изотермического и изохорно-изотермического потенциалов.

D G = D H – T D S, D F = D U – T D S;

D H = D G + T D S, D U = D F + T D S,

где D H иD U – изменение полной энергии в системе при р = const и V = const соответственно; D G иD F – энергия, которая связана с производством полезной работы; T D S – энергия, которая перешла в энергию хаотичного (теплового) движения частиц, вследствие чего она уже не может перейти в работу.

Поэтому D G иD F называют еще свободной энергией, а T D S – связанной энергией.

Т а б л и ц а

Дата добавления: 2013-12-11