
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Миноры и алгебраические дополнения
|
|
|
|
МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ. ПРАВИЛО КРАМЕРА.
Def. Пусть дан определитель 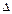 n -го порядка. Выберем в нем произвольные k строк и k столбцов (
n -го порядка. Выберем в нем произвольные k строк и k столбцов (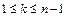 ). Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель этой матрицы называют минором k-го порядка (М) определителя
). Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель этой матрицы называют минором k-го порядка (М) определителя  .
.
Def. Если вычеркнуть строки и столбцы, на пересечении которых находится минор М, то оставшиеся элементы образуют матрицу порядка n-k, определитель которой называется дополнительным минором к минору М и обозначается  .
.
В частности, дополнительный минор к элементу 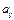 обозначается
обозначается  .
.
Def. Пусть минор k -го порядка расположен в строках с номерами 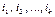 и в столбцах с номерами
и в столбцах с номерами 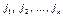 . Обозначим
. Обозначим
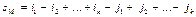
Алгебраическим дополнением для минора М называют число 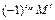 .
.
В частности, алгебраическое дополнение к элементу 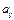 обозначается
обозначается  и
и 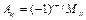 .
.


 N. Пусть дан определитель
N. Пусть дан определитель 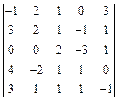 .
.
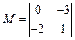 – минор 2-го порядка,
– минор 2-го порядка, 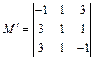 – дополнительный минор к
– дополнительный минор к 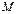 ,
, 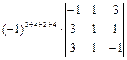 – алгебраическое дополнение для
– алгебраическое дополнение для 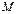 .
.
Смысл алгебраического дополнения становится ясен из следующей леммы.
| Lemma | Произведение любого минора определителя 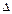 на его алгебраическое дополнение есть сумма, слагаемые которого являются некоторыми членами определителя на его алгебраическое дополнение есть сумма, слагаемые которого являются некоторыми членами определителя
|
Доказательство.
1) Рассмотрим сначала случай, когда выбранный минор k -го порядка расположен в верхнем левом углу определителя.


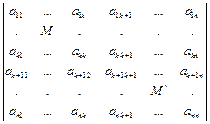
Произвольный член минора М имеет вид 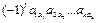 , где l – число инверсий в перестановке
, где l – число инверсий в перестановке 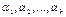 . Произвольный член его дополнительного минора
. Произвольный член его дополнительного минора 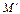 имеет вид
имеет вид 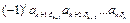 , где t – число инверсий в перестановке
, где t – число инверсий в перестановке 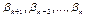 .
.
Члены алгебраического дополнения будут получены из членов минора  умножением на
умножением на 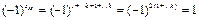 , т.е. будут равны членам дополнительного минора.
, т.е. будут равны членам дополнительного минора.
Произведение членов 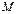 и
и 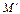 имеют вид
имеют вид 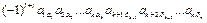 .
.
Элементы 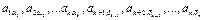 расположены в разных строках и разных столбцах определителя. Найдем знак, с которым входит произведение
расположены в разных строках и разных столбцах определителя. Найдем знак, с которым входит произведение 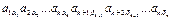 в определитель. Для этого определим число инверсий в перестановке
в определитель. Для этого определим число инверсий в перестановке 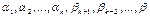 . Все
. Все 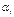 принимают значения от 1 до k, а принимают значения от k+ 1 до n, поэтому между собой
принимают значения от 1 до k, а принимают значения от k+ 1 до n, поэтому между собой 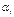 и
и 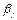 не будут образовывать инверсии и общее число инверсий равно l+t, т.е. слагаемые, входящие в произведение
не будут образовывать инверсии и общее число инверсий равно l+t, т.е. слагаемые, входящие в произведение 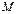 и
и 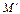 равны членам определителя.
равны членам определителя.
2) Рассмотрим общий случай. Пусть минор 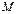 расположен в строках с номерами с номерами
расположен в строках с номерами с номерами 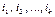 и в столбцах с номерами
и в столбцах с номерами 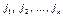 .
.
Переставляя строки и столбцы определителя, передвинем минор 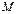 в верхний левый угол. Для этого
в верхний левый угол. Для этого 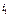 строку поменяем местами со всеми предыдущими, передвинув на первое место, т.е. выполним
строку поменяем местами со всеми предыдущими, передвинув на первое место, т.е. выполним 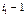 транспозицию.
транспозицию.
Для того, чтобы строка 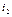 заняла второе место, подвергнем ее
заняла второе место, подвергнем ее 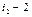 транспозиции и т.д.,
транспозиции и т.д., 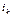 строку подвергнем
строку подвергнем 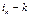 транспозициям. Всего транспозиций строк:
транспозициям. Всего транспозиций строк: 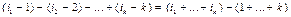 . В результате минор М будет расположен в первых k строках.
. В результате минор М будет расположен в первых k строках.
Далее последовательно переставляем столбцы: 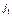 , пока он не займет первое место,
, пока он не займет первое место, 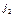 , пока он не займет второе место и т.д. Имеем всего
, пока он не займет второе место и т.д. Имеем всего 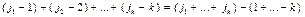 транспозиций столбцов. Полученный определитель отличается от исходного множителем
транспозиций столбцов. Полученный определитель отличается от исходного множителем 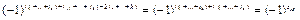 . Согласно доказанному в первом случае, произведение
. Согласно доказанному в первом случае, произведение  состоит из слагаемых, входящих в состав определителя.
состоит из слагаемых, входящих в состав определителя. 
| Th.4.1 | (теорема Лапласа) Сумма произведений всех миноров k-го порядка, расположенных в выбранных строках, на соответствующие им алгебраические дополнения равно определителю. |
Доказательство.
 – суммa нескольких слагаемых определителя. Пересчитаем число всех таких слагаемых в произведении всех миноров k -го порядка, расположенных в выбранных строках.
– суммa нескольких слагаемых определителя. Пересчитаем число всех таких слагаемых в произведении всех миноров k -го порядка, расположенных в выбранных строках.
Число слагаемых в миноре k -го порядка равно 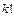 , число слагаемых в его алгебраическом дополнении
, число слагаемых в его алгебраическом дополнении 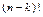 . Тогда
. Тогда  содержит
содержит 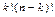 слагаемых.
слагаемых.
Количество миноров k -го порядка в выбранных строках равно 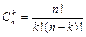 . Значит, сумма произведений всех миноров k -го порядка, расположенных в выбранных строках, на их алгебраические дополнения содержит
. Значит, сумма произведений всех миноров k -го порядка, расположенных в выбранных строках, на их алгебраические дополнения содержит  слагаемых, т.е. равна соответствующему определителю.
слагаемых, т.е. равна соответствующему определителю. 
Теоремы 4.2 и 4.3 являются следствиями теоремы Лапласа.
| Th.4.2 | (разложение определителя по строке или столбцу)
Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т.е.
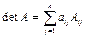 (4.1) или (4.1) или 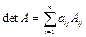 (4.2) (4.2)
|
Формула 4.1 называется разложением определителя по элементам строки, а формула 4.2 – разложением определителя по элементам столбца.
| Th.4.3. | (Определитель с углом нулей)
  Пусть Пусть 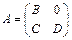 , где B – матрица размера , где B – матрица размера 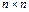 и D – матрица размера и D – матрица размера 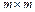 . тогда . тогда 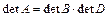 . .
|
Доказательство.
Для доказательства достаточно разложить определитель по теореме Лапласа, выбирая миноры n -го порядка в первых n строках.
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1839; Нарушение авторских прав?; Мы поможем в написании вашей работы!