Свойства определителей

Свойства определителей

Def.Транспонированием матрицы (определителя) называется такое ее преобразование, при котором ее строки становятся столбцами с теми же норами. Для матрицы А транспонированная матрица обозначается .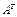

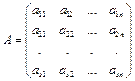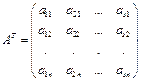Если , то (3.1)

Теоремы 3.1 – 3.8 выражают свойства определителей n -го порядка.

Th.3.1

Определитель не меняется при транспонировании.

Доказательство.

Очевидно в результате транспонирования элементы, стоящие в разных строках и столбцах, остаются также в разных строках и столбцах. Пусть в 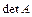входит слагаемое 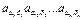, тогда это же слагаемое будет входить и 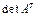в . В 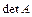ему будет соответствовать подстановка 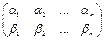, а в 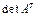- подстановка 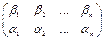. Очевидно обе подстановки имеют одинаковую четность. Значит, 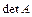и 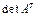состоят из одних и тех же слагаемых, т.е. равны.

Замечание. Теорема 3.1. позволяет сделать вывод о равноправии строк и столбцов в определителе. Поэтому, доказательство остальных свойств будем проводить только для строк.

Th.3.2

Определитель, в котором одна строка (или столбец) состоит из нулей, равен нулю.

Доказательство.

Пусть в определителе все элементы i -ой строки равны нулю. Очевидно, что в каждое слагаемое определителя будет входить один элемент из i -ой строки, а поскольку они все нулевые, то определитель обращается в нуль.

Th.3.3

Если в определителе поменять местами две строки (два столбца), то определитель изменит знак на противоположный.

Доказательство.

Пусть дан определитель, в котором поменяли местами i -ю и j -ю строки:

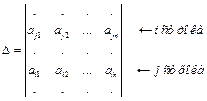(3.2)

Пусть 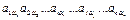– произвольное слагаемое исходного определителя. Ему соответствует подстановка:

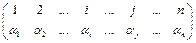(3.3)

В преобразованный определитель это слагаемое также входит, поскольку все множители остались в различных строках и столбцах, и ему соответствует подстановка:

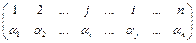(3.4)

Подстановки (3.3) и (3.4) имеют различную четность, т.к. получаются друг из друга с помощью одной инверсии в верхней строке. Значит, слагаемые вида 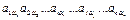будут входить в полученный определитель с противоположным знаком, т.е. определитель поменяет знак.

Th.3.4

Если определитель содержит две равные строки (столбца), то он равен нулю..

Доказательство.

Пусть определитель равен 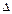. Поменяем местами две равные строки. С одной стороны, согласно теореме 3.3, его значение станет равным 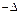, а с другой стороны не изменится. Имеем 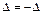, откуда .

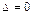Th.3.5

Если все элементы некоторой строки (столбца) определителя умножить на число k, то определитель умножится на k.

Доказательство.

.

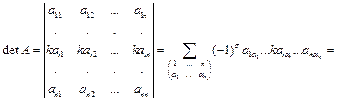
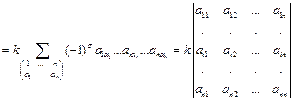Замечание. Теорема 3.5 позволяет выносить из какой-либо строки (столбца) общий множитель за знак определителя.

Th.3.6

Если определитель содержит две пропорциональные строки(столбца), то он равен нулю.

Доказательство.

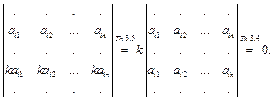
Th.3.7

Если все элементы некоторой строки (столбца) определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементами этой строки (столбца) служат первые слагаемые, а во втором – вторые слагаемые. Все остальные элементы совпадают с элементами исходного определителя.

Доказательство.

.

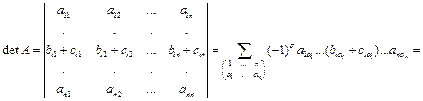
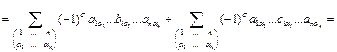
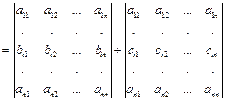Th.3.8

Если к какой-нибудь строке (столбцу) определителя прибавить другую строку, умноженную на произвольное число, то определитель не изменится.

Доказательство.

Прибавим к i -й строке j -ю строку, умноженную на число k. Получим:

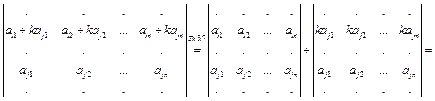
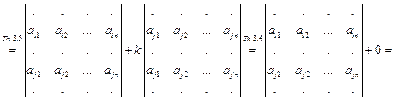
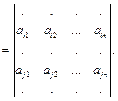
Def. Матрица, у которой все элементы, стоящие под (над) главной диагональю равны 0 называют верхней треугольной (нижней треугольной) матрицей.

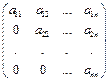Верхняя треугольная матрица

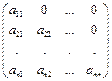Нижняя треугольная матрица

Th.3.9

Определитель верхней треугольной матрицы равен произведению элементов главной диагонали.

Доказательство.

Докажем, что 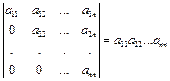. (3.5)

Очевидно, что произведение 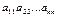будет одним из слагаемых определителя, взятым со знаком «+», т.к. соответствующая ему подстановка 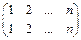– четная.

Пусть – произвольное слагаемое определителя, не равное 0. Тогда 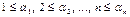(поскольку элементы, у которых 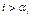, расположены ниже главной диагонали, т.е. равны 0). Но 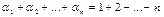. Значит, 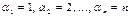. Таким образом, определитель содержит лишь одно ненулевое слагаемое .

Следствие. Определитель нижней треугольной матрицы равен произведению элементов главной диагонали, т.е.

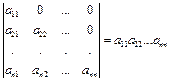. (3.6)

Дата добавления: 2013-12-12