Определитель n-го порядка

Def. Определителем n-го порядка называется число, равное алгебраической сумме 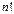слагаемых, каждое из которых представляет произведение 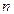множителей, взятых по одному и только по одному из каждой строки и каждого столбца. Причем каждое слагаемое входит в сумму со знаком «+», если подстановка, состоящая из индексов множителей четная, и со знаком
«–», если эта подстановка нечетная, т.е.:

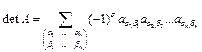(2.5)

или

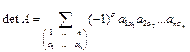, (2.6)

где 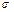– общее число инверсий в обеих строках подстановки.

В частности, определитель второго порядка 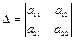будет содержать два слагаемых: 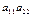и 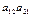. Определим знаки этих слагаемых. Подстановка из индексов слагаемого 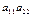имеет вид 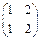и является четной. Значит, это слагаемое входит в определитель со знаком «+». Подстановка из индексов, соответствующая слагаемому 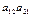имеет вид 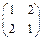и является нечетной. Т.е. второе слагаемое входит в определитель со знаком «–». Таким образом,

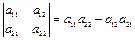
(2.7)

Т.е. определитель второго порядка равен разности произведения элементов главной диагонали и элементов побочной диагонали.

Аналогично, определитель третьего порядка содержит 3!=6 слагаемых и вычисляется по формуле:

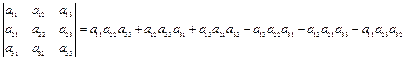(2.8)

Убедитесь самостоятельно в правильности знаков слагаемых в формуле (2.8). Для запоминания этой формулы используют схему:

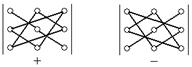
Рис. 2.1. Схема вычисления определителя третьего порядка

Существует удобный способ вычисления определителя третьего порядка с помощью так называемого правила Саррюса. Допишем справа к определителю первые два столбца, а далее будем перемножать элементы, стоящие на одних диагоналях так, как показано на рисунке 2.2.

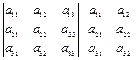– – – + + + Рис. 2.2 Правило Саррюса для вычисления определителя третьего порядка

Вычисление определителей более высоких порядков по определению представляется очень громоздким. Уже определитель 4-го порядка будет содержать 4!=24 слагаемых, а определитель 5-го порядка уже 5!=120 слагаемых. Далее мы сформулируем свойства определителей, которые облегчат их вычисление.

Дата добавления: 2013-12-12