
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства сложения векторов
|
|
|
|
Основные понятия векторной алгебры
ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНОЙ АЛГЕБРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ И ИХ СВОЙСТВА. ЛИНЕЙНО ЗАВИСИМЫЕ (НЕЗАВИСИМЫЕ) СИСТЕМЫ ВЕКТОРОВ. БАЗИС. КООРДИНАТЫ ВЕКТОРА.
Физические величины можно разделить на два вида: скалярные и векторные. Скалярные величины характеризуется числом при данной единице измерения. Такими величинами, например, являются масса, температура, площадь, плотность и т.д.
Def. Величины, которые характеризуются неотрицательным числом при данной единице измерения (модулем) и направлением, называются векторными.
Векторные величины обычно изображают направленными отрезками.
Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.
Def. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец.
Направленный отрезок обозначается 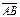 .
.
Def.Модулем 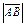 направленного отрезка
направленного отрезка 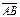 называется длина отрезка АВ.
называется длина отрезка АВ.
На чертеже направленный отрезок 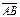 снабжен стрелкой на конце.
Def. Направленные отрезки снабжен стрелкой на конце.
Def. Направленные отрезки 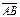 и и 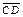 называются одинаково направленными или сонаправленными, (обозначается называются одинаково направленными или сонаправленными, (обозначается 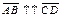 ), если каковы бы ни были равные ), если каковы бы ни были равные
|  Рис. 10.1
Рис. 10.1
|
отрезки 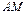 и
и 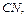 содержащие точки
содержащие точки 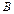 и
и 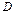 соответственно, расстояние
соответственно, расстояние 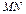 не превосходит некоторого данного расстояния (рис. 10.2).
не превосходит некоторого данного расстояния (рис. 10.2).
Очевидно, что сонаправленные отрезки лежат на параллельных прямых или на одной прямой.
Def. Направленные отрезки 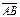 и и 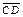 называют противоположно направленными (пишут называют противоположно направленными (пишут 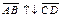 ), если они лежат на параллельных прямых или на одной прямой и не являются сонаправленными.
Направленные отрезки ), если они лежат на параллельных прямых или на одной прямой и не являются сонаправленными.
Направленные отрезки 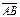 и и 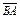 называются противоположными. называются противоположными.
| 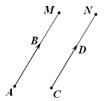 Рис. 10.2
Рис. 10.2
|
Def. Если начало и конец направленного отрезка совпадают, то его называют нулевым направленным отрезком. Его модуль считается равным нулю, а направление не определено.
Def. Два направленных отрезка 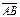 и
и 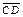 считаются равными, если они сонаправлены и имеют равные длины. (Обозначают
считаются равными, если они сонаправлены и имеют равные длины. (Обозначают 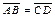 ).
).
Def. Множество всех равных направленных отрезков называется вектором (или свободным вектором).
Так понимаемый вектор называется свободным, поскольку он представляется направленным отрезком независимо от того, от какой точки тот отложен. Равные направленные отрезки 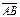 и
и 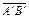 , отложенные от разных точек представляют один и тот же вектор. Поэтому говорят:
, отложенные от разных точек представляют один и тот же вектор. Поэтому говорят: 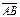 – это вектор
– это вектор  , отложенный от точки А.
, отложенный от точки А.
Def. Направление равных направленных отрезков называется направлением вектора, а их модуль – модулем вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс равных направленных отрезков.
Def. Если 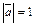 , то вектор
, то вектор  называется единичным вектором или ортом. Def. Множество нулевых отрезков называется нулевым вектором
называется единичным вектором или ортом. Def. Множество нулевых отрезков называется нулевым вектором 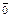 . Его длина равна нулю, а направление не определено.
. Его длина равна нулю, а направление не определено.
Def. Вектор 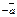 называется противоположным вектору
называется противоположным вектору  , если они имеют равные модули и противоположно направлены.
, если они имеют равные модули и противоположно направлены.
Т.е. если вектор 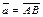 , то вектор
, то вектор 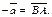
Def. Сонаправленные и противоположно направленные векторы называются коллинеарными. Обозначают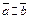 . Нулевой вектор считается коллинеарным любому вектору.
. Нулевой вектор считается коллинеарным любому вектору.
Def. Три (или более) вектора называются компланарными, если они параллельны некоторой плоскости.
Линейные операции над векторами и их свойства
Def. Пусть даны два вектора  и
и 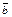 . Из произвольной точки
. Из произвольной точки 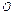 пространства отложим
пространства отложим 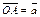 и
и 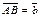 . Тогда
. Тогда 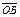 есть направленный отрезок и значит, определяет вектор
есть направленный отрезок и значит, определяет вектор 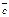 , который называют суммой векторов
, который называют суммой векторов  и
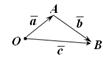
и 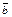 (рис. 10.3). Пишут:
(рис. 10.3). Пишут: 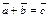
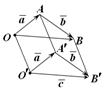
Покажем, что вектор 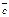 не зависит от выбора точки O. Для этого выберем другую точку
не зависит от выбора точки O. Для этого выберем другую точку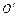 . Пусть
. Пусть 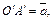
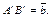 Тогда
Тогда 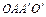 – параллелограмм. Аналогично,
– параллелограмм. Аналогично, 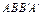 – параллелограмм
– параллелограмм 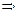
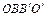 – параллелограмм
– параллелограмм 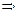
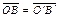 , т.е. они определяют один и тот же вектор
, т.е. они определяют один и тот же вектор  .
.
| 
|
|
| Рис. 10.3 | Рис. 10.4 | Рис. 10.5 |
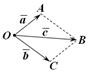
Способ сложения векторов, изложенный выше (рис. 10.3), называется правилом треугольника. Можно также использовать правило параллелограмма (рис. 10.5).
1. 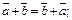 (10.1)
2. (10.1)
2. 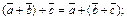 (10.2)
3. (10.2)
3. 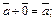 (10.3)
4. (10.3)
4. 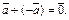 (10.4) (10.4)
|
Доказательство свойств 1-2 представлено на рис. 10.6, 10.7. Свойства 3-4 вытекают непосредственно из определения суммы векторов.
Def. Произведением вектора  на число
на число 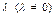 называется вектор
называется вектор 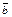 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) векторы  и
и 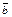 сонаправлены, если
сонаправлены, если 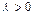 и противоположно направлены, если
и противоположно направлены, если 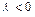 ;
;
2) 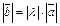 .
.
Произведение  на число 0 есть нулевой вектор. Пишут:
на число 0 есть нулевой вектор. Пишут: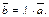
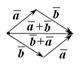 Рис. 10.6
Рис. 10.6
| 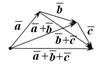 Рис. 10.7
Рис. 10.7
| 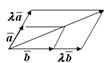 Рис. 10.8
Рис. 10.8
|
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 699; Нарушение авторских прав?; Мы поможем в написании вашей работы!