
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проекция вектора на ось
|
|
|
|
ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Def. Прямая называется осью, если на ней задано положительное направление. Направление оси задается вектором 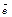 (направляющий вектор оси).
(направляющий вектор оси).
Def. Пусть задана некоторая ось 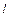 и точка
и точка 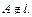 Проведем
Проведем 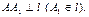 Точка
Точка 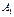 называется проекцией точки
называется проекцией точки 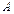 на ось
на ось 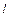 (рис. 11.1)
(рис. 11.1)
Def. Пусть 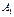 - проекция точки
- проекция точки 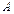 на ось
на ось 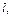 а
а 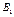 - проекция точки
- проекция точки 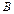 на ось
на ось 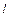 (рис. 11.2)Тогда
(рис. 11.2)Тогда 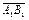 называется векторной проекцией
называется векторной проекцией 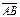 на ось
на ось 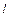 (на вектор
(на вектор 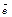 ).
).
Def. Скалярной проекцией (или проекцией) вектора 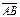 на ось
на ось 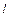 (на вектор
(на вектор 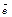 ) называется число, равное
) называется число, равное 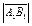 и взятое со знаком плюс, если
и взятое со знаком плюс, если 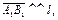 и со знаком минус, если
и со знаком минус, если 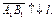 Обозначают
Обозначают 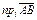 или
или 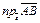 . Т.е.
. Т.е.
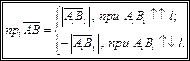 (11.1)
(11.1)
Легко видеть, что 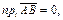 если
если 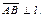
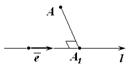 Рис. 11.1
Рис. 11.1
| 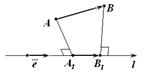 Рис. 11.2 Рис. 11.2
| 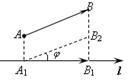 Рис. 11.3
Рис. 11.3
|
| Th.11.1 | (свойства проекции вектора на ось)
1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью, т.е.
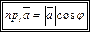 (11.2)
2. При умножении вектора на число его проекция на ось также умножается на это число, т.е. (11.2)
2. При умножении вектора на число его проекция на ось также умножается на это число, т.е.
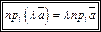 (11.3)
3. Проекция суммы векторов на ось равна сумме проекций слагаемых, т.е. (11.3)
3. Проекция суммы векторов на ось равна сумме проекций слагаемых, т.е.
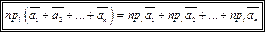 (11.4) (11.4)
|
Доказательство.
1. Действительно, пусть 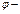 уго между
уго между 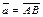 и
и 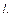 Если
Если 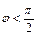 (рис. 11.3), то
(рис. 11.3), то 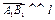 , поэтому
, поэтому
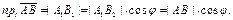
Если 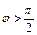 (рис. 11.4), то (рис. 11.4), то 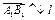 и и
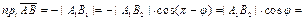 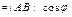  . .
| 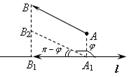 Рис. 11.4
Рис. 11.4
|
2. Если 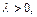 то
то 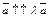 (рис. 11.5). Тогда:
(рис. 11.5). Тогда:
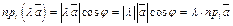
 .
.
Если 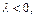 то
то 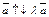 (рис. 11.6). В этом случае имеем:
(рис. 11.6). В этом случае имеем:
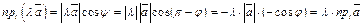
 .
.
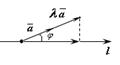 Рис. 11.5
Рис. 11.5
| 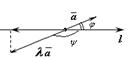 Рис. 11.6
Рис. 11.6
| 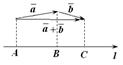 Рис. 11.7
Рис. 11.7
|
3. Доказательство проведем для двух слагаемых. Возможны два случая.
Если проекции обоих векторов положительные числа (рис. 11.7), то 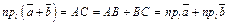
 .
.
Если одна из проекций отрицательна (рис. 11.8), то 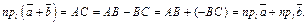 Что и требовалось доказать Что и требовалось доказать  .
Замечание. Данное свойство можно обобщить на любое конечное число слагаемых. .
Замечание. Данное свойство можно обобщить на любое конечное число слагаемых.
| 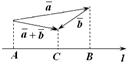 Рис. 11.8
Рис. 11.8
|
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 374; Нарушение авторских прав?; Мы поможем в написании вашей работы!