
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы координат. Геометрический смысл декартовой прямоугольной
|
|
|
|
Геометрический смысл декартовой прямоугольной
Геометрический смысл декартовой прямоугольной системы координат выражается следующей теоремой.
| Th.11.2 | Если 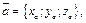 то то 
|
Доказательство.
Пусть  . Через конец вектора точку . Через конец вектора точку 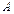 проведем плоскости параллельные координатным плоскостям проведем плоскости параллельные координатным плоскостям  Точки пересечения этих плоскостей с осями Точки пересечения этих плоскостей с осями 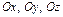 обозначим соответственно обозначим соответственно 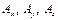 (рис. 11.9). Очевидно (рис. 11.9). Очевидно
 С другой стороны
С другой стороны  Значит, Значит,

| 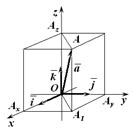 Рис. 11.9
Рис. 11.9
|
Но  Теорема доказана
Теорема доказана  .
.
Следствие. Если 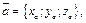 то
то
 (11.5)
(11.5)
Доказательство вытекает из формулы длины диагонали в прямоугольном параллелепипеде.
Def. Обозначим углы, которые образует вектор  с координатными осями
с координатными осями 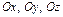 через
через  соответственно.
соответственно.  называются направляющими косинусами вектора
называются направляющими косинусами вектора 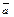
Из треугольника 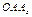 (рис. 11.9):
(рис. 11.9):
 (11.6)
(11.6)
Аналогично получаем
 (11.7)
(11.7)
Нетрудно увидеть, что
 (11.8)
(11.8)
Скалярное произведение векторов
Def. Скалярным произведением векторов называют число, равное произведению их модулей на косинус угла между ними. Обозначают  или
или  Т.е.
Т.е.
 (11.9)
(11.9)
где 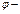 угол между
угол между  и
и 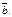
Из формулы (11.9) имеем:
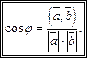 (11.10)
(11.10)
Согласно (11.2) 
Заменяя  по формуле (11.10), получаем:
по формуле (11.10), получаем:
 (11.11)
(11.11)
Соотношение (11.11) можно записать и в таком виде:
 (11.12)
(11.12)
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 1193; Нарушение авторских прав?; Мы поможем в написании вашей работы!