Def. Величину , равную отношению половины фокального расстояния к действительной полуоси называют эксцентриситетом гиперболы

Т.е. для гиперболы с фокусами на оси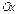

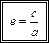(16.19)

Причем, 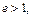т.к.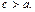

Эксцентриситет характеризует форму гиперболы. Действительно,

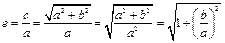
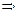
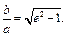(16.20)

Из (16.20) следует, что если 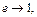то 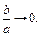Значит, чем меньше 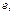тем меньше отношение 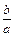ее полуосей. А значит, более вытянут основной прямоугольник вдоль оси .

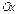Для равносторонней гиперболы 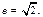Действительно,

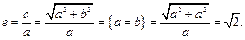
Понятно, что для гиперболы с фокусами на оси 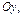заданной уравнением (16.15), эксцентриситет равен:

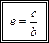(16.21)

При выводе канонического уравнения гиперболы мы получили следующие выражения для фокальных радиусов:

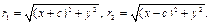
Используя понятие эксцентриситета, можно получить рациональные выражения для фокальных радиусов. Действительно, из (16.10)

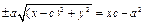
Разделим обе части равенства на 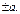Получим 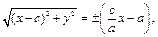т.е.

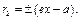(16.22)

Для правой ветки гиперболы

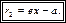(16.23)

Учитывая, что для правой ветки гиперболы 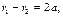получаем, что

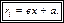(16.24)

Для левой ветки гиперболы

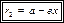(16.25)

и 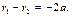Тогда:

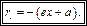(16.26)

КРИВЫЕ ВТОРОГО ПОРЯДКА (продолжение)

Дата добавления: 2013-12-12