
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Директрисы эллипса и гиперболы
|
|
|
|
Def. Прямые, перпендикулярные большой оси эллипса и расположенные на расстоянии 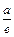 от его центра, называются директрисами эллипса.
от его центра, называются директрисами эллипса.
Если задан эллипс своим каноническим уравнением 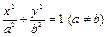 с фокусами на оси
с фокусами на оси 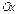 (т.е.
(т.е. 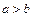 ), то его директрисами будут прямые
), то его директрисами будут прямые 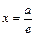 и
и 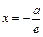 . Поскольку для эллипса
. Поскольку для эллипса 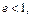 то
то 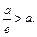 Значит, директрисы не пересекают эллипс (рис. 17.1).
Значит, директрисы не пересекают эллипс (рис. 17.1).
Аналогично определяется директриса гиперболы.
Def. Прямые, перпендикулярные действительной оси гиперболы и расположенные на расстоянии 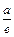 от его центра, называются директрисами гиперболы.
от его центра, называются директрисами гиперболы.
Для гиперболы 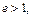 значит,
значит, 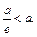 Следовательно, директрисы не пересекают гиперболу. Для гиперболы, фокусы которой расположены на оси абсцисс, директрисы изображены на рис. 17.2.
Следовательно, директрисы не пересекают гиперболу. Для гиперболы, фокусы которой расположены на оси абсцисс, директрисы изображены на рис. 17.2.
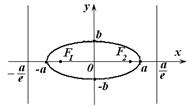 Рис. 17.1
Рис. 17.1
| 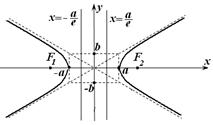 Рис. 17.2
Рис. 17.2
|
| Th. 17.1 | Пусть 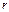 - длина фокального радиуса точки эллипса (гиперболы), а - длина фокального радиуса точки эллипса (гиперболы), а 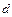 - расстояние от этой точки до соответствующей директрисы, тогда - расстояние от этой точки до соответствующей директрисы, тогда
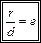 (17.1) (17.1)
|
Доказательство.
Проведем доказательство теоремы для эллипса.
Пусть 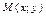 текущая точка эллипса. Согласно (16.8) и (16.9)
текущая точка эллипса. Согласно (16.8) и (16.9) 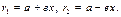 Очевидно, что
Очевидно, что 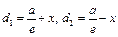 (рис. 17.3).
(рис. 17.3).
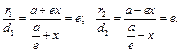 Что и требовалось доказать. Аналогично проводится доказательство для правой и левой ветвей гиперболы Что и требовалось доказать. Аналогично проводится доказательство для правой и левой ветвей гиперболы  . .
| 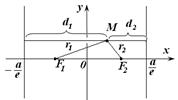 Рис. 17.3
Рис. 17.3
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 347; Нарушение авторских прав?; Мы поможем в написании вашей работы!