Поверхности второго порядка

Def.Поверхностью второго порядка называется множество точек пространства, определяемое в некоторой прямоугольной декартовой системе координат уравнением второй степени:

(18.1)

После применения движения и, возможно, умножения уравнения на ненулевой коэффициент, уравнение поверхности в трехмерном пространстве приводится к одному из следующих видов:

1. (эллипсоид)

2. 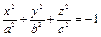(мнимый эллипсоид)

3. (однополостной гиперболоид)

4. (двуполостной гиперболоид)

5. (конус)

6. 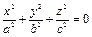(мнимый конус)

7. (эллиптический параболоид)

8. (гиперболический параболоид)

9. 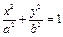(эллиптический цилиндр)

10. (мнимый цилиндр)

11. 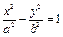(гиперболический цилиндр)

12. 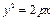(параболический цилиндр)

13. (пара пересекающихся плоскостей)

14. (пара мнимых пересекающихся плоскостей)

15. (пара параллельных плоскостей)

16. (пара мнимых параллельны плоскостей)

17. (пара совпадающих плоскостей)

Дата добавления: 2013-12-12