
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гиперболический параболоид
Def. Гиперболическим параболоидом называется поверхность, каноническое уравнение которой имеет вид
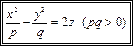 (18.13)
(18.13)
Исследуем форму гиперболического параболоида.
1. Из уравнения (18.13) видно, что координатные плоскости 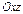 и
и 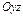 являются плоскостями симметрии гиперболического параболоида, а ось
являются плоскостями симметрии гиперболического параболоида, а ось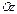 – его осью симметрии.
– его осью симметрии.
2. Исследуем форму эллиптическогопараболоида при 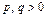 по его сечениям координатными плоскостями и параллельными им плоскостями. Линией пересечения гиперболического параболоида с плоскостью
по его сечениям координатными плоскостями и параллельными им плоскостями. Линией пересечения гиперболического параболоида с плоскостью 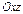 будет парабола
будет парабола
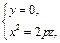 (18.14
(18.14
а с плоскостью 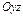 - парабола
- парабола
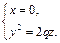 (18.15)
(18.15)
Плоскости 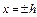 пересекают гиперболический параболоид по параболам
пересекают гиперболический параболоид по параболам
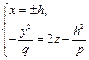
или
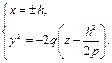 (18.16)
(18.16)
Эти параболы представляют собой результат паарллельного переноса параболы (18.15), при котором ее вершина перемещается из точки 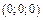 в точки
в точки 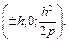 Т.е. гиперболический параболоид может быть образован путем параллельного переноса параболы (18.15), при котором ее вершина движется по параболе (18.14).
Т.е. гиперболический параболоид может быть образован путем параллельного переноса параболы (18.15), при котором ее вершина движется по параболе (18.14).
3. Линия пересечения гиперболического параболоида с плоскостью 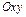 задается уравнением
задается уравнением
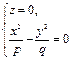
или
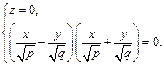 (18.17)
(18.17)
Уравнение (18.17) задает пару пересекающихся прямых.
Линии персечения гиперболического параболоида с плоскостями 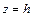 представляют собой при
представляют собой при 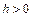 гиперболу
гиперболу
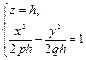 с действительной полуосью
с действительной полуосью 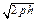 и мнимой полуосью и мнимой полуосью 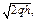 а при а при 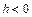 гиперболу гиперболу
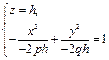
| 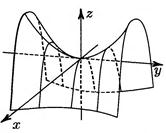 Рис. 18.5
Рис. 18.5
|
с действительной полуосью 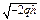 и мнимой полуосью
и мнимой полуосью 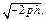
Гиперболический параболоид изображен на рис. 18.5.
|
|
Дата добавления: 2013-12-12; Просмотров: 490; Нарушение авторских прав?; Мы поможем в написании вашей работы!