
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конические поверхности
|
|
|
|
Def.Конической поверхностью (конусом) называется поверхность, образованная прямыми, проходящими через данную точку 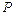 и пересекающими данную линию и пересекающими данную линию 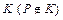 (рис. 18.10). Эти прямые называются образующими конуса, точка (рис. 18.10). Эти прямые называются образующими конуса, точка 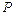 – вершиной конуса, а кривая К – направляющей конуса.
Def. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением – вершиной конуса, а кривая К – направляющей конуса.
Def. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной декартовой системе координат задается уравнением
| 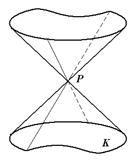 Рис. 18.10
Рис. 18.10
|
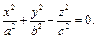 (18.18)
(18.18)
Покажем, что если точка 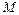 (отличная от начала координат) лежит на конусе второго порядка, то все точки прямой
(отличная от начала координат) лежит на конусе второго порядка, то все точки прямой 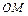 (
(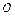 – начало координат) также лежит на конусе. Пусть
– начало координат) также лежит на конусе. Пусть 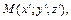
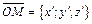 – направляющий вектор прямой
– направляющий вектор прямой 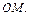 Согласно (15.2) координаты произвольной точки
Согласно (15.2) координаты произвольной точки 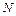 удовлетворяют соотношениям
удовлетворяют соотношениям
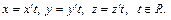
Очевидно, что координаты точки 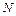 удовлетворяют уравнению (18.18), т.е. точка
удовлетворяют уравнению (18.18), т.е. точка 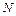 лежит на поверхности конуса. Что и требовалось доказать.
лежит на поверхности конуса. Что и требовалось доказать.
Исследуем форму эллипса по его сечениям координатными плоскостями и плоскостями параллельными им.
1. Линия пересечения конуса второго порядка плоскостью 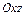 задается уравнением
задается уравнением
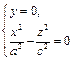 или
или 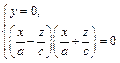 (18.19)
(18.19)
Уравнение (18.19) задает пару пересекающихся прямых.
Аналогично можно установить, что плоскость 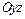 пересекает конус второго порядка также по двум пересекающимся прямым.
пересекает конус второго порядка также по двум пересекающимся прямым.
2. Уравнения линий пересечения конуса второго порядка с плоскостями 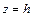 имеют вид имеют вид
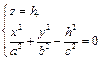 или
или
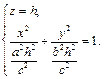 (18.20)
Уравнение (18.20) задает эллипс с полуосями (18.20)
Уравнение (18.20) задает эллипс с полуосями 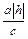 и и 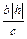 , причем с возрастанием , причем с возрастанием 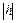 значение полуосей увеличивается. Изображение конуса значение полуосей увеличивается. Изображение конуса
| 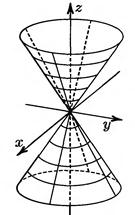 Рис. 18.11
Рис. 18.11
|
второго порядка представлено на рис. 18.11.
Def. Если в уравнении (18.18) 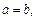 то сечения конуса второго порядка плоскостями
то сечения конуса второго порядка плоскостями 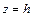 – окружности. Такой конус называется круглым.
– окружности. Такой конус называется круглым.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 340; Нарушение авторских прав?; Мы поможем в написании вашей работы!