Интегральная теорема Муавра-Лапласа

Центральная предельная теорема

Центральная предельная теорема устанавливает предельную форму композиции распределений случайных величин при неограниченном увеличении числа случайных величин, входящих в композицию.

Теорема Ляпунова (Центральная предельная теорема). Пусть Х ₁, Х ₂, Х ₃,…, Х_n – последовательность независимых одинаково распределенных случайных величин 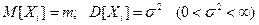и пусть

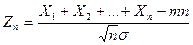
Тогда, при любом ,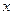

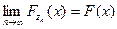где F (x)=0,5+ Ф (х) - функция распределения стандартной случайной величины.

Практически это означает, что при сформулированных выше условиях распределение случайно величины Z_n асимптотически приближается к стандартному нормальному распределению N (0;1²). Следовательно, для случайной величины Z_n можно приближенно использовать все формулы, которые справедливы для стандартного нормального распределения, в частности, для любых α и β:

P (α < Z_n < β)≈ Ф (β)- Ф (α), причем согласно центральной предельной теореме, точность этого приближенного равенства возрастает с увеличением n.

Рассмотрим систему n испытаний Бернулли с вероятностью успеха 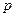в каждом испытании. В этом случае вероятность m успехов вычисляется по формуле Бернулли, прямое использование которой затруднено при больших n (n >10).

Рассмотрим приближенную формулу для вычисления вероятности того, что число успехов содержится в пределах от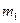до : .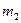

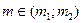Представим величину m как сумму случайных величин ξ ₁+ ξ ₂+…+ ξ_n (индикаторы успеха):

m = ξ ₁+ ξ ₂+…+ ξ_n

Учитывая, что M [ m ]= np, D [ m ]= npq, введем случайную величину

,

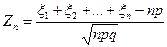распределение которой, согласно центральной предельной теореме, асимптотически (при n →∞) приближается к стандартному нормальному распределению N (0;1²).

Поэтому

.

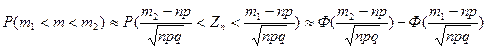Эта формула называется интегральной теоремой Муавра-Лапласа.

Пример 3.1..2. Серия Бернулли содержит n =100 испытаний, причем вероятность появления события A в каждом испытании равна р =0,8. Найти вероятность того, что число успехов 75≤ m ≤90.

Решение:

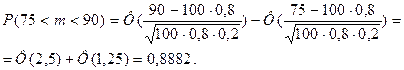
Дата добавления: 2013-12-11